Logo

菜单

[DC-DC01]BUCK变换器分析与推导

Fenice Liu
Fenice Liu
发布于 2024-11-05 / 64 阅读
1
0

[DC-DC01]BUCK变换器分析与推导

#电力电子#DC-DC#电路原理分析#控制理论应用

在日常的电子开发过程中，降压是一个经常的需求，当然了目前市场上有许许多多的产品例如集成了开关器件的Converter和只具有环路控制的Controller芯片，辅助以厂商提供的数据表和选型工具(例如MPS DC-DC在线设计工具)可以很轻松的画出原理图和选型。但是在进行需要自主抉择的选型和一些要求严格的状况(极高的转换效率或者极大的输出功率——往往是不友好的电流)的情况下，我们仍然需要知道这背后的选型原理，并且Buck-Boost变换器几乎是入门DC-DC开关电源的“大头守卫”。

1.BUCK变换器原理分析

Buck变换器（降压变换器）是一种常用的直流-直流（DC-DC）转换器，用于将较高的输入直流电压转换为较低的输出直流电压。它广泛应用于电源管理系统中，如电池供电设备、开关电源和电力电子系统。Buck变换器是一种高效、紧凑的DC-DC转换器，能够有效地降低电压并提供稳定的输出。它在现代电子设备中发挥着重要的作用，尤其是在对电源效率要求高的应用场合。通过合理设计和优化，Buck变换器能够满足不同负载条件下的电源需求。

a.BUCK变换器原理图

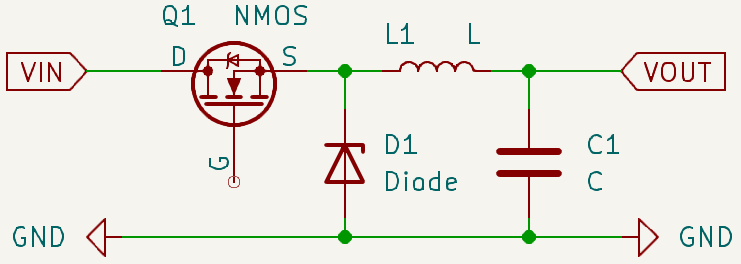
buck-schematic.png

上图即为BUCK变换器最经典的原理图拓扑，这里需要说明的是一个可用的BUCK变换器肯定不止这些，即使不谈乱七八糟的保护和驱动电路，至少控制开关器件Q1的开关管的栅极和测量输出电压Vout以及构建二者反馈的控制电路途中是肯定没有的，上图仅仅是考虑了核心的拓扑以及被动工作器件。突然看到这样一大堆（其实也就是4个）器件可能会一脸懵逼，我们来逐个考虑这些器件究竟处于什么样的目的被添加又为什么不得不添加——这对于阅读文献了解新拓扑和理解更加复杂的拓扑更加有利：

  1. 我们的核心目的是将高电压Vin转换Vout输出，并且不同于最简单的电阻分压的方法，这种方法应该能够某种程度上无视后级电路的负载变换而“理想的”维持住输出电压的稳定性。出于最朴素的想法：后级电路对于功率的要求应当是均匀变化的，也就是其功率曲线应当表现出平滑特征——那么我们是不是可以参照PWM调光这种思路，例如从5V降压为3.3V就可以66%的时间供电而34%的时间不供电？

  2. 实现步骤0的想法非常简单：我们使用开关器件Q1，它可以是个N-MOS也可以是个P-MOS，甚至可以是个手动开关！而这就像是帧数高了PPT也能变成视频一样——只要我们的开关频率足够快，后级电路从宏观上就感知不到关闭电源的空档期。在此基础上我们为了这个核心想法加入C1电容器作为储能器件——这就像是一个蓄水池，能够某种程度上抹平波动。

  3. 但是加入了电容C1之后我们会发现一个问题：现实之中没有理想开关器件Q1，器件开关是有难度和开销的：假设在放电周期中C1上的电平从Vin下降一段产生了压差ΔV那么在开通Q1的一瞬间，由于极大的压差和近乎短路的阻抗，以及最重要的——电容两端电压不可以突变的条件，Q1就会流过一个超大的足以损毁它自身的电流。而直接在输出回路上加上一个限流电阻虽然能够解决问题——但是带来了更大的问题——一个巨大的损耗引起的足以让王安石自杀的效率系数！那么这个时候好朋友楞次定律出场——加上一个电感器L1实现限制电流变化率从而限制瞬时大电流！

  4. 又但是，加入了电感器之后出现了更加严重的问题——楞次定律的一体两面：电感流过的电流不可以突变，这就让Q1关断时L1上的电流急剧减小而其会引发一个巨大的足以直接击穿Q1的电势差(右侧被电容C瞬时钳位，电势差通过左侧点击穿Q1放电)从而损坏Q1。所以我们需要给L1加入一个续流泄放支路——显然这个支路不能直接影响Q1开通时的电流环路，所以加入一个二极管D1。

加入了这些元件之后，完成BUCK变换器的核心议题就是：如何控制开关器件Q1的开通-关断比例和频率从而控制输出电压值。在此基础上我们将会进行一系列针对于各个元件和工作流程的分析，从而丰富这一拓扑结构的意涵和控制策略以及元件选型策略的完善性，我们将在本节中优先分析工作原理。

b.伏-秒平衡/安-秒平衡

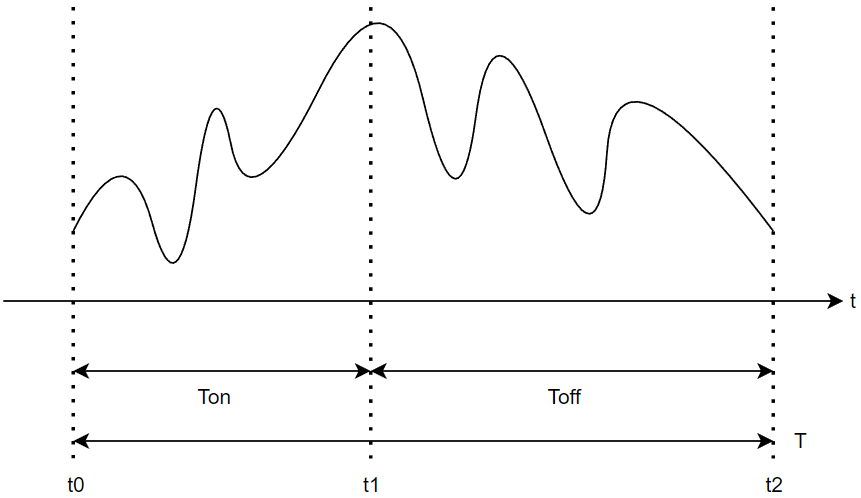
buck-balance.png

本小节要讨论的核心是伏-秒平衡法则(Voltage-Second Balance Rule)，与之对偶的推论也可以称为安-秒法则，这个法则不仅仅适用于BUCK变换器也不仅仅适用于DC-DC电路分析——事实上它是具有强烈的一般性的，但是这一法则在开关电源相关电路分析中会特别有用，推导这个理论的过程之中我们要明确以下几个很明显但是容易被忽视的条件：

  • 对于理想电容器(Ideal Capacitor)的欧姆定律变例：电容两端的电压因为电荷不能瞬移所以不能突变也就是i=C\frac{du}{dt}

  • 对于理想电感器(Ideal Conductor)的欧姆定律变例：电感上流过的电流因为电磁感应的楞次定律不能突变也就是u=L\frac{di}{dt}

  • 讨论的前提是系统工作在稳态(Steady State)也就是具有周期性的变化而非不具有周期性的不稳定的暂态(Transient State)

图中给出的曲线是电感上流过的电流或者电容两端的电压随时间变化的周期性曲线的一个周期的状态，我们此处为保持论证的不失一般性而不讨论具体的变化曲线解析式。对于电感器而言，通过简单的微积分处理开关器件的开通相(Phase On)：

\begin{aligned} u(t)&=L\frac{di(t)}{dt}\tag{1-1}\\ u(t)dt&=Ldi(t)\\ \int_{t_0}^{t_0+t_{on}}u(t)dt&=\int_{i(t_0)}^{i(t_0+t_{on})}Ldi(t)=L[i(t_0+t_{on})-i(t_0)]\\ i(t_1)&=i(t_0)+\frac1L\int_{t_0}^{t_0+t_{on}}u(t)dt \end{aligned}

那么对于开关器件的关断相(Phase off)进行同等的分析可知：

\begin{aligned} u(t)&=L\frac{di(t)}{dt}\tag{1-2}\\ u(t)dt&=Ldi(t)\\ \int_{t_1}^{t_1+t_{off}}u(t)dt&=\int_{i(t_1)}^{i(t_1+t_{off})}Ldi(t)=L[i(t_1+t_{off})-i(t_1)]\\ i(t_2)&=i(t_1)+\frac1L\int_{t_1}^{t_1+t_{off}}u(t)dt \end{aligned}

考虑到电流变化的讨论前提——周期性的变化，并且发现t_0=0的选择不失去一般性，可以得到伏-秒平衡法则：

\begin{aligned} i(t_0)&=i(t_2)\tag{1-3}\\ -\frac1L\int_{t_1}^{t_1+t_{off}}u(t)dt&=i(t_0)+\frac1L\int_{t_0}^{t_0+t_{on}}u(t)dt\\ 0&=\int_{t_0}^{t_0+t_{on}+t_{off}}u(t)dt\\ \int_0^Tu(t)dt&=0 \end{aligned}

按照同样的分析方法，分析电容两端电压的变化可以得到电容上流过的电流的结论：

\int_0^Ti(t)dt=0\tag{1-4}

因此我们可以这样总结，在周期性的电路运作之中，针对理想电容器和理想电感器(没有寄生电感，寄生电容，并且ESR=0)：

  • 一个周期内电感器两端电压的变化对时间的积分为0，一个周期内电容器上流过的电流的变化对时间的积分为0

  • 这体现了L/C作为理想储能元件条件下，能量(电磁势能)守恒定律和质量(电荷)守恒定律在电路分析之中的投射

c.系统工作状态分析

buck-schematic.png

回到BUCK变换器的这张核心的拓扑图，我们同样使用一个周期内分为T=t_{on}+t_{off}也就是开关器件Q1开通和关断的两个时段的分析框架之中，以电感L1为核心器件进行分析，各个器件的状况为：

  • Q1开通，分析时忽略Rds-on带来的开通损耗，认为Q1相当于短路导线

  • D1反向截至，忽略漏电流和从正向偏置到反向偏置过程中的变化以及损耗

  • L1电流不断增大被充能，电能在L1上转换为磁能存储在L之中

  • C1被充电，电流由上而下流入C1，电能被存储在C1之中

因此可以得到电路方程，其中u_o代表输出电压——小写字母代表变化函数，大写变量代表常量：

\begin{aligned} u_o(t)&=u_C(t)\tag{1-5}\\ &=V_{in}-u_L(t)=V_{in}-L\frac{di(t)}{dt}\\ Ldi(t)&=V_{in}dt-u_o(t)dt\\ L\int_{i(t_0)}^{i(t_0+t_{on})}di(t)&=\int_{t_0}^{t_0+t_{on}}V_{in}dt-\int_{t_0}^{t_0+t_{on}}u_o(t)dt\\ I_{peak}&=I_{t_0}+\frac1L\left(V_{in}t_{on}-\int_{t_0}^{t_0+t_{on}}u_o(t)dt\right) \end{aligned}

我们将时刻t1的电流也就是充电结束时最大的电流称为Ipeak，接着我们来看Q1关断相位的器件状况：

  • Q1关断，分析时忽略寄生电容和漏电流带来的对后级的影响和损耗，认为Q1相当于断点，前级电源整体被切除

  • D1正向偏置导通，不考虑输入电平VIN小于D1的导通电压的状况，不考虑正向偏置过程中的变化认为Q1关断时D1就饱和导通

  • L1上正向电流不能突变，L1从用电器变成电源，右侧电压高于左侧开始放电，磁能转换为电能放出

  • 由于L1左侧点被D1钳位到低电平+导通压降的电平值，右侧输出电压一定低于充电相位的电平值，事实上被电容C1钳位，这样可以确定电感的放电速度也就是电流的变化速率

  • C1开始放电，存储在C1之中的电能被放出到负载端

因此可以得到电路方程：

\begin{aligned} u_o(t)&=u_C(t)\tag{1-6}\\ &=-[u_L(t)+u_D(t)]=-[L\frac{di(t)}{dt}+u_D(t)]\\ Ldi(t)&=-[u_o(t)dt+u_D(t)dt]\\ L\int_{i(t_1)}^{i(t_1+t_{off})}di(t)&=-\int_{t_1}^{t_1+t_{off}}u_o(t)dt-\int_{t_1}^{t_1+t_{off}}u_D(t)dt\\ I_{t_2}&=I_{t_0}=I_{peak}+\frac1L\left(-\int_{t_1}^{t_1+t_{off}}u_o(t)dt-V_Dt_{off}\right) \end{aligned}

结合式(1-5)与式(1-6)可以得到输出电压与输入电压以及时间系数的关系：

\begin{aligned} V_{in}t_{on}-V_Dt_{off}&=\int_{t_0}^{t_0+t_{oon}}u_o(t)dt+\int_{t_1}^{t_1+t_{off}}u_o(t)dt\tag{1-7}\\ V_{in}t_{on}-V_Dt_{off}&=\int_{t_0}^{t_0+T}u_o(t)dt\\ V_{out}T&=V_{in}t_{on}-V_Dt_{off}\\ V_{out}&=V_{in}D-V_D(1-D),D=\frac{t_{on}}{T} \end{aligned}

上式之中，V_D代表输出电压的平均值，也就是“抹平”视角下观测到的输出电压同样也是我们设计的输出电压；同时定义了一个全新的参数D为开通时间与周期时间的比值，也就是我们通常说的占空比。可以看到当我们认为D1为理想二极管的状况下，也就是V_D=0的情况下这个公式十分符合直觉，输出电压就是输入电压乘以占空比，所以可以粗略地说开关器件的占空比就是输出电压与输入电压之比。

2.BUCK变换器工况与元件选型

仅仅了解BUCK变换器的拓扑和工作原理是不足的，任何电子设计的知识最终都要落实到工程实现，当我们试图在PCB上实装一个BUCK变换器的时候我们会碰到各种问题，从元器件的选型到引脚连接，到各种保护电路，再到焊接调试和用户反馈充满了各种各样意想不到的问题，这其中比较经典的也是卡住第一步的问题就在于，如何确认需求？如何将需求转化为具体参数？如何将参数与元器件关联？因此在本节之中主要探讨这样几个具有显著性的问题：

  • BUCK拓扑中的功率电感如何选择感值和过流能力？这与最终电源的输出纹波电流有何关系？

  • BUCK拓扑中的输出电容如何选择容值和种类材质？这与最终电源的输出纹波电压有何关系？

  • BUCK拓扑基本电路中不包含的输入电容为什么大家都在用？具体有什么作用怎么选择？

  • 为什么有的BUCK电路是直接使用半桥驱动器？他们的续流二极管去哪里了？什么是同步整流？

a.纹波电流与输出电感

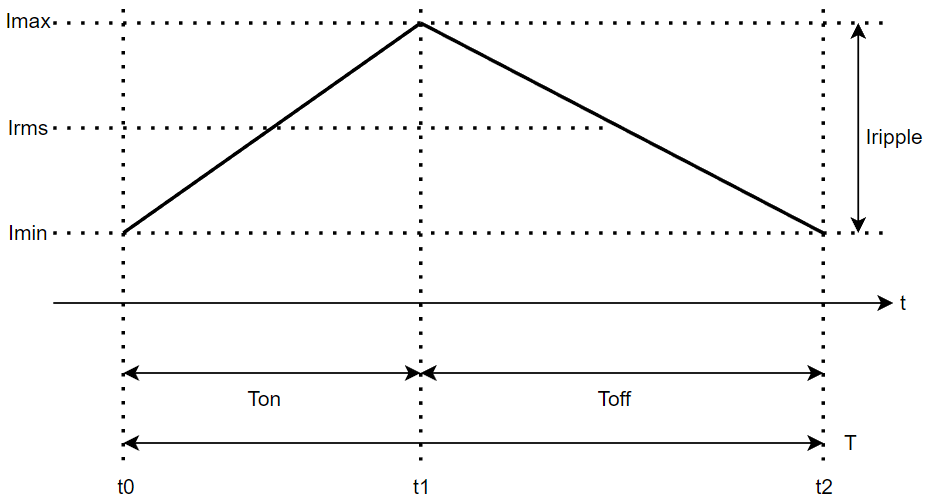
buck-current.png

通过前文工作原理和充放电相位流程的分析，我们以L1为核心不难得到如上的电感电流变化曲线图：

  • 以下做出讨论时认为L1是一个理想电感，C1是一个理想电容，D1是一个理想二极管也就是不考虑导通压降，这个参数在当今BUCK变换器基本都是同步整流半桥结构的状况下意义不大，并且即使真的使用一个二极管其对于相关计算的影响也微乎其微，甚至不如裕度预留值或者器件本身的制造误差值大，没有分析必要

  • 因为讨论的是输出稳态，所以令周期开始时间t_0=0不会对讨论和推证的一般性造成影响

  • 变化曲线仅仅是示意图，实际使用中不可能出现这样理想的三角波(起码电流求导就会出现连续但是不可导)，而是一个近似三角波的曲线，使用这样的近似曲线在有助于计算的同时并不会带来过大的分析误差

  • 对于输出电压u_o(t)的积分，粗略的使用不严谨的中值定理，也就是认为任意一段时间的积分等于其均方根值乘以时间长度，这也就是认为输出电压是一个理想的三角波，理由和合理性同上条所述

首先讨论纹波电流的概念，也就是输出电流之中的周期性变化的交流部分I_{ripple}也就是我们说的纹波电流，通过式(1-5)可知：

\begin{aligned} I_{ripple}&=I_{max}-I_{min}\tag{2-1}\\ &=I_{t_{on}}-I_0\\ &=\frac1L\left(V_{in}t_{on}-\int_{0}^{t_{on}}u_o(t)dt\right)\\ &=\frac1L(V_{in}t_{on}-V_{out}t_{off})\\ &=\frac TL(V_{in}\frac{t_{on}}T-V_{out}\frac{t_{off}}T)\\ &=\frac{V_{in}D(1-D)}{f_{sw}L},f_{sw}=\frac1T \end{aligned}

通过上式的推导，可以看到纹波电流的计算值具有以下特性：

  • 开关频率f_{sw}越高也就是开关周期越小，带来的纹波电流值就越小

  • 电感的感值也就是储能能力(并不是储能绝对值，功率约算公式为W(t)=\frac12Li^2(t))越大，纹波电流越小

  • 输入电压越高，给转换电路带来的压力也就越大，充放电电流越大导致了纹波电流越大

  • 纹波电流值与输出/输入比D有关，整体呈现一个二次函数，当输出电压为输入电压的一半，纹波压力最大

那么接下来我们还需要确认电感的载流能力以保证尖峰电流能够顺利的通过电感，首先我们需要计算流过电感的均方根值，这也就对应电感的额定电流（并非极限值，极限值应当对应尖峰值）过流能力。由于负载的整体阻抗大小与功率角可能多变，分析时，我们假定负载带来的电流均方根为I_{out}那么有：

\begin{aligned}\tag{2-2} I_{out}&=\frac1T\int_0^Ti_o(t)dt\\ i_L(t)&=i_c(t)+i_o(t)\\ I_{rms}&=\frac1T\int_0^T[i_o(t)+i_C(t)]dt\\ &=\frac1T\int_0^Ti_o(t)dt+\frac1T\int_0^Ti_C(t)dt\\ &=\frac1T\int_0^Ti_o(t)dt=I_{out} \end{aligned}

在以上的推导中我们发现前文提到的安-秒平衡起到了作用(事实上如果我们一开始就假定电流电压变化为三角波那么伏-秒平衡将会直接得出占空比就是电压比的结论，然而这种讨论不具有一般性，然而这里我们并未假定任何前提讨论仍然具有一般性)，我们发现流入流出电容的电流值在对于整个周期的积分上整体为0，因此电感的额定过流也就是均方根为输出电流本身，那么我们不难算出最大电流值：

I_{max}=I_{rms}+\frac12I_{ripple}\tag{2-3}

然而此处仍旧存在的问题是：如何计算纹波极限值对应的极小电感值呢？那么我们这样定义纹波率r和纹波极限值R并且根据这个定义算出最小需要的输出电感L1的最小感值L_{min}：

\begin{aligned}\tag{2-4} r&=\frac{I_{ripple}}{I_{rms}}\times 100\%\\ &=\frac{V_{in}D(1-D)}{I_{out}f_{sw}L}\times 100\%\\ r\le R&\rightarrow L\ge\frac{V_{in}D(1-D)}{I_{out}f_{sw}R} \end{aligned}

通过推导过程不难发现，如果丝毫不控制L的值那么电流纹波率最大将达到200%，这是完全不可接受的，工程上一般认为20~30%的纹波率是一个正常器件能够忍受的范围。然而，这也不是说电感值的选取越大越好，过大的电感将带来：封装过大而使PCB布局布线艰难，价格的极速上升，更大的EMI问题(这个问题在过高的开关频率下也存在)等等。综上所述，选取电感的步骤为：

  • 确定输入电压范围(带有反馈的BUCK转换器一般是宽压)，取其中的上界作为输入电压V_{in}以便计算极限参数

  • 确定输出电压的值(这个值一般比较精确，如果是可调宽压范围那么应当取最接近0.5倍率的值)这样就可以计算占空比D

  • 通过查阅芯片DataSheet或者自行决定(分立元件自制)得到最大的开关频率作为f_{sw}

  • 计算额定功率从而得到额定输出电流，如果功率变化较大，那么应当取较大的电流值而非平均值

  • 通过式(2-2~2-4)计算电感额定电流值，最大电流值，最小感值，并且留出足够的制造误差裕度选择实际的电感

b.纹波电压与输出电容

合适的选择电感能够降低变换器的纹波电流，但是显然含有纹波的不只有输出电流，还有与电容C1并联的输出电压，从信号分析的角度上来说，变换器的输出包括一个直流分量和一个交流分量，也就是符合：

\begin{cases}\tag{2-5} i_L(t)&=i_c(t)+i_o(t)\\ &=i_{AC}(t)+i_{DC}(t)\\ i_c(t)&=C\frac{du_c(t)}{dt}\\ &=i_{AC}(t)=i_L(t)-I_{out} \end{cases}

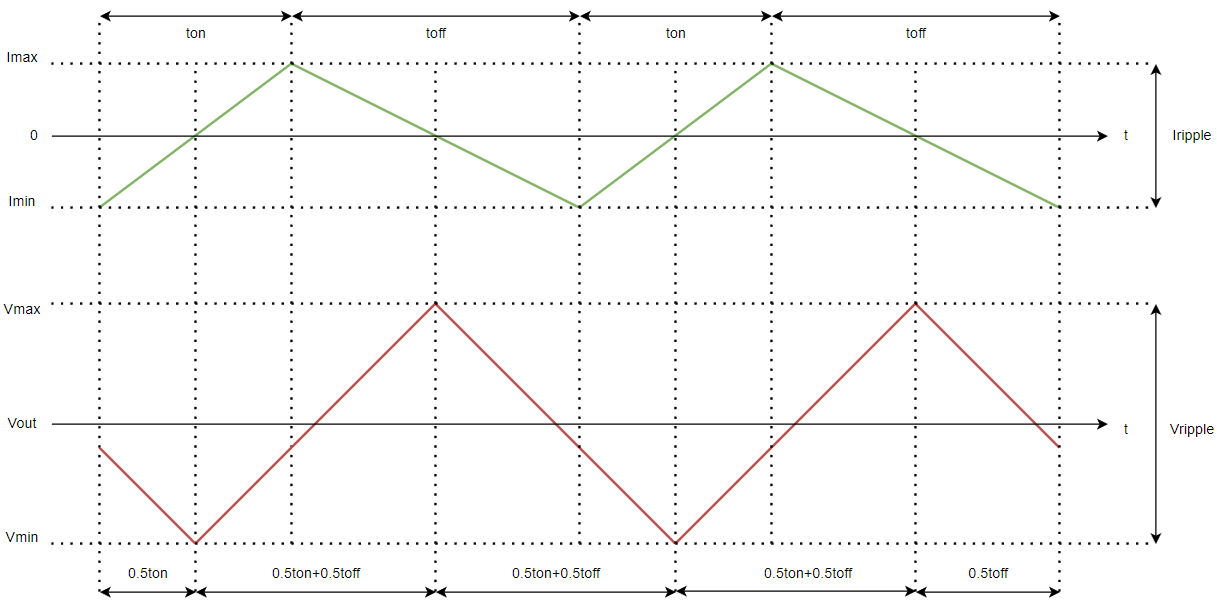
buck-voltage.png

如上图所示，绿色曲线为电容C1上流过的电流的曲线，总体来说就是积分为0的输出电流的交流分量也就是Iripple，而由于电容的功率角为滞后四分之一个相位，可以预见到红色曲线也就是C1两侧的电压曲线，也就是输出电压曲线，整个的充放电过程为：

  • t=t0时刻，Q1开通，然而在L1充电的过程中，电容仍然不断对后级供电，电压降低，直到降低到L1上的电流满足供电需求

  • t=t0+0.5ton时刻停止放电，开始被L1充电，电压开始上升

  • t=t0+ton时刻，Q1关断，然而在L1的放电过程中，电容仍然在不断被L1充电， 电压升高，直到L1上电流无法满足供电需求

  • t=t0+0.5T时刻停止充电，开始对后级电路供电，电压开始下降

整个充放电过程的分析基于后续电路负载为纯阻性，如果后续负载的功率角不是0度，那么电压和电流的滞后关系将会被改变，例如后续负载如果还是容性那么滞后可能加大，如果后续的负载呈现出感性那么这个滞后程度可能会减小，但是无论如何我们可以分析出纹波电压Vripple以及对应前文纹波电流定义的纹波率以及达到纹波率R需要的最小电容值：

\begin{aligned}\tag{2-6} V_{ripple}&=\int_{t_0+\frac12t_{on}}^{t_0+\frac12T}\frac1Ci_C(t)dt=\frac12\cdot\frac{I_{ripple}}2\cdot\frac T2\cdot\frac1C\\ &=\frac{I_{ripple}}{8Cf_{sw}}=\frac{V_{in}D(1-D)}{8LCf^2_{sw}}\\ r&=V_{ripple}/V_{out}\times100\%=\frac{(1-D)}{8LCf^2_{sw}}\times100\%\\ r\le R&\rightarrow C\ge\frac{(1-D)}{8Lf^2_{sw}R} \end{aligned}

上式之中的积分通过面积法快速求出，可以得到这样几个结论：

  • BUCK变换器的开关频率越高，同等纹波率需要的输出电容容值越小，但是过高的开关频率带来EMI问题

  • 需要的纹波率越小，输出电容的容值就越大，这一结论符合直觉

  • 输入-输出电压的差值越大需要的输出电容容值越大，这里的差值指的是比例而与具体的电压值无关，而输出电压值影响的参数是电容的耐压参数，也就是输出电压为额定电压而加上50%的纹波为最大值

  • 输出电容的容值与电感值相关，越大的感值就要求越小的容值，因此应当先选择输出电感再选择输出电容

上述结论之中非常令人感兴趣的一点就是，输出电容的选择居然与另一个器件输出电感的感值L相关而不是仅仅与BUCK变换器的具体参数相关这是为什么呢？假设我们从自动控制理论的角度来看问题，减小输出纹波实际上要求的是一件什么事情？其实是保留直流分量而尽量减小交流分量，也就是说本质是一个低通滤波器，而L1-C1就形成了一个LC滤波器，我们也就是需要滤除f_{sw}以及更高频率的干扰，而考虑到一个经典的LC滤波器其截止频率为f=1/2\pi\sqrt{LC}那么这个公式所表现出的原理就很好理解了。综上所述选取电容的步骤为：

  • 电容材质优先选择陶瓷电容的X5R和X7R标准，考虑温度系数和偏置系数，避免使用劣质的Y5V和Z5U

  • 如果需求容值极大找不到单个可用电容，可以考虑并联扩容方案，万不得已也可以考虑高品质的铝电解电容

  • 尽量不要使用钽电容，钽电容脆弱的耐压性以及对于di/dt的羸弱抗性可能导致其直接损毁

  • 优先选取输出电感L，计算输出电感L后设定电压纹波率参数R并且带入公式计算即可，其他参数选择L时全部确定

  • 经验上考虑温升损耗和制造性误差，一般考虑将耐压条件(V_{out}+\frac12V_{ripple})和容值条件留出30%-50%的裕度

  • 选型时可以关注电容的ESR(Equal-Serial Resistance,串联等效电阻)，经验上要求不大于1/(8Cf_{sw})否则由于串联等效电阻引起的电压波动就会与纹波电压达到同一数量级，那么前面的计算就会出现巨大的偏差

c.电源去耦与输入电容

在通常的BUCK变换器经典电路的使用始终，我们会发现在输入电源上并联了一个电容，这个电容通常被称为输入电容，这是由于输入电源本身的不理想性和BUCK电路元件的不理想性所需要的，对于一个理想直流电压源而言：

  • 电源不存在内阻，因此伏安特性曲线表现为完全的常值函数

  • 电源完全纯净，也就是输入的电压和电流仅仅存在直流分量而不存在交流分量

  • 电源供电能力无限大，可以输出任意大小的电流带动任意大小的负载

而实际情况是：

  • 电源存在内阻，其伏安特性曲线往往随着复杂加重电流变大而产生电压损耗

  • 电源并不纯净，电源本身就含有一定的交流分量(例如上级电源本身来源于一个直流开关电源的输出)并且会因为开关器件的工作导致耦合更多的高次谐波反向污染电源

  • 电源并不能隔离，如果一个电源接入多个DC-DC变换器，那么其他变换器在上条之中提到的高次谐波污染可能会随着公共电源线倒灌耦合到本BUCK之中

  • 电源负载能力有限，假设我们的转换为12V/5V输出电流3A电源效率100%那么可以计算得出输入电源的输入电流应当为1.25A，然而这是一个RMS值。在开关器件关断时不需要电流，而开关器件开通时需要比1.25A更大的电流，那么如果电源本身的供电能力接近这一边界值就可能导致高负载时输出不正常

综上所述需要使用一个电容并联在输入电源的两端，一旦并联这一电容可以实现：

  • 无论Q1开通或者关断，电源间歇不断的向包括输入电容和BUCK在内的后级电路输出电流，这样可以大大改善开关引起的高次谐波对电源的干扰

  • 电容在Q1开通期间可以辅助电源进行供电 ，这样对于电源的输出电流带载能力的要求下降，能够让电源工作在更加有力的负载状态下，提高稳定性

  • 电容本身可以滤除电源中自带的交流部分，也就是降低输入电压源的纹波电流；也可以滤除反向污染的交流部分，降低各种方面的耦合提高瞬态响应能力

因此我们考虑这样一个简单的结构：

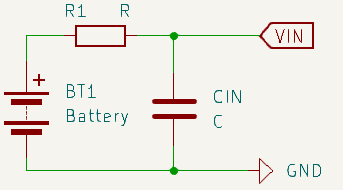
buck-cin.png

其中BT1代表电压源之中真正的理想电源部分，R1代表电源内阻，CIN代表我们的输入电容。可以看到当VIN之中的Q1开通时CIN和BT1一起向后级电路供电，而Q1关断时BT1通过R1向CIN充电，也就是相当于一个RC网络的充放电问题，这就要求：

  • Q1关断期间，要使得BT1提供的电流尽量保持稳定，要求C的容量较大不能在下次Q1开通之前就完成充电，这样还是会造成输入电流的断续

  • Q1开通期间，CIN要有足够的输出电荷能力，不能在下次Q1关断之前就完全放电，这样会造成电源同时给VIN和C1充电的更加恶劣的供电需求

  • 因此得出结论，RC电路的时间常数要足够大，起码大于关断间隔Toff

首先我们可以根据能量守恒定律计算出在占空比D和电源效率\eta下的输入电流需求：

\begin{aligned}\tag{2-7} P_{out}&=\eta P_{in}\\ I_{out}V_{out}&=\eta I_{in}V_{in}\\ I_{in}&=\frac{D}{\eta}I_{out} \end{aligned}

而由于我们考虑了电源内阻的存在并且在模型之中添加了RC网络，那么随着后级电路之中Q1开通和关断，输入到Q1的电压V_{in}的直流分量上面显然叠加着一个交流分量，我们称这个交流分量为输入纹波电压，定义为\Delta V_{in}。而通过安-秒平衡法则我们可以发现在开通和关断相位中流入留出CIN的电流总量(对时间积分)相等，并且考虑我们设计CIN的目的是平稳输入电流，因此将I_{in}认为是闭合期间的电容流入电流，这样可以计算出开通期间电容对后级充电分担电源压力的电流I_{in,on}也就是：

\begin{aligned}\tag{2-8} I_{in}\times t_{off}&=I_{in,on}\times t_{on}\\ I_{in,on}&=\frac {1-D}DI_{in}=\frac{1-D}\eta I_{out} \end{aligned}

那么根据这个电流需求辅以时间间隔就可以算出电荷量进而得出最小要求的输入电容：

\begin{aligned}\tag{2-9} C_{in}&=\frac{\Delta Q}{\Delta V_{in}}\\ &=\frac{I_{in,on}t_{on}}{\Delta V_{in}}=\frac{D(1-D)I_{out}}{\eta\Delta V_{in}f_{sw}} \end{aligned}

可以看到：

  • 电容的最小容值通过式(2-9)进行计算，考虑容量误差等原因最好按照150%值选型，耐压值为叠加纹波的输入电压

  • 输入电容对于材质要求不高，可以选择具有性价比的电解电容，能够在单个封装中做到较大容量

  • 计算输入电容前需要确定输出电压(占空比)，额定输出电流，开关频率以及电源效率系数(这个参数由于选型时容值至少按照150%选择而大多数BUCK设计效率不会低于66.67%事实上可以忽略)

d.同步整流与半桥驱动

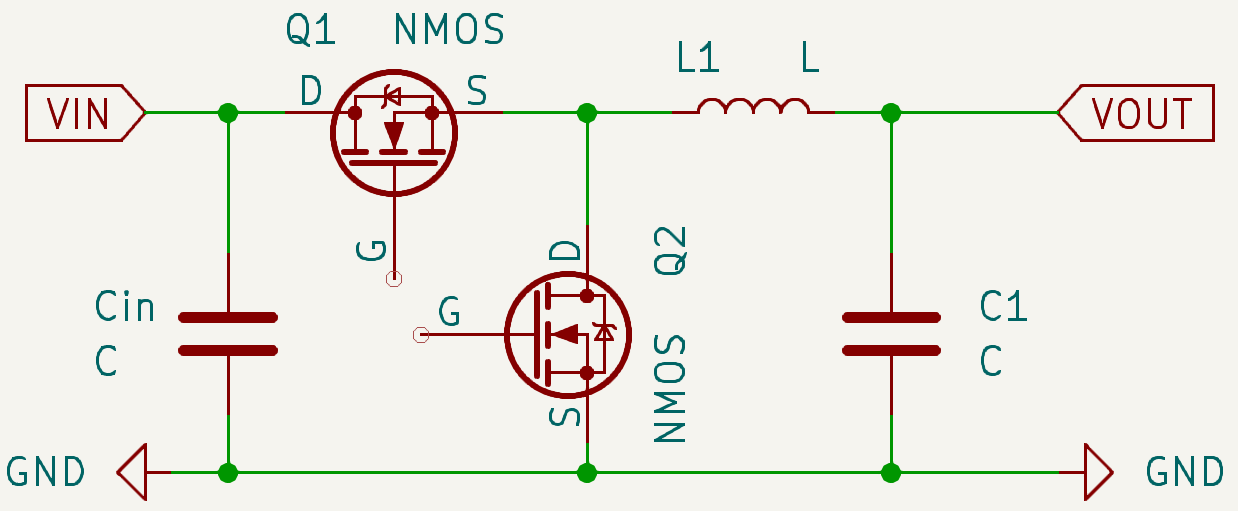
buck-sync.png

在传统的BUCK变换器拓扑之中，也就是所谓的异步整流(Asynchronous Rectification)模式，使用普通二极管作为整流元件，而在上图之中的拓扑之中将D1替换为一个MOS管进行整流，这个MOSFET的开通和关断是通过Gate控制的，也就是通过控制电路同步控制开通关闭，所以被称为同步整流(Synchronous Rectification)。其优点主要有：

  • 提高效率，如果使用传统的硅管D1在导通时会带来0.7V或者锗管D1在导通时会带来0.1~0.4V的压降，假设续流电流为1A那么带来的损耗就是0.7W或者0.1~0.4W。而使用MOSFET时一旦管子开通并且进入稳态那么导通损耗电阻Rds_on就非常小，能控制到mΩ级别——那么对应的即使续流电流为10A级别，功率损耗也不会超过1W

  • 减少热量，更小的管损会带来更低的散热压力，对于PCBA整体的温度控制会显著低于异步整流方式，那么对于各个元件在非线性区的温升偏移会有相当大的改善

在同步整流时由于我们要同时控制一个半桥（两个开关管）那么对于驱动运算压力和电气上的风险性会增高，例如我们在统一时刻将Q1和Q2一起开通就会导致VIN通过两个极低的导通电阻对地放电，过大的电流将会烧毁开关器件甚至将前级电路损坏。为了防止这一问题，我们采用”带有死区的互补驱动信号“处理：

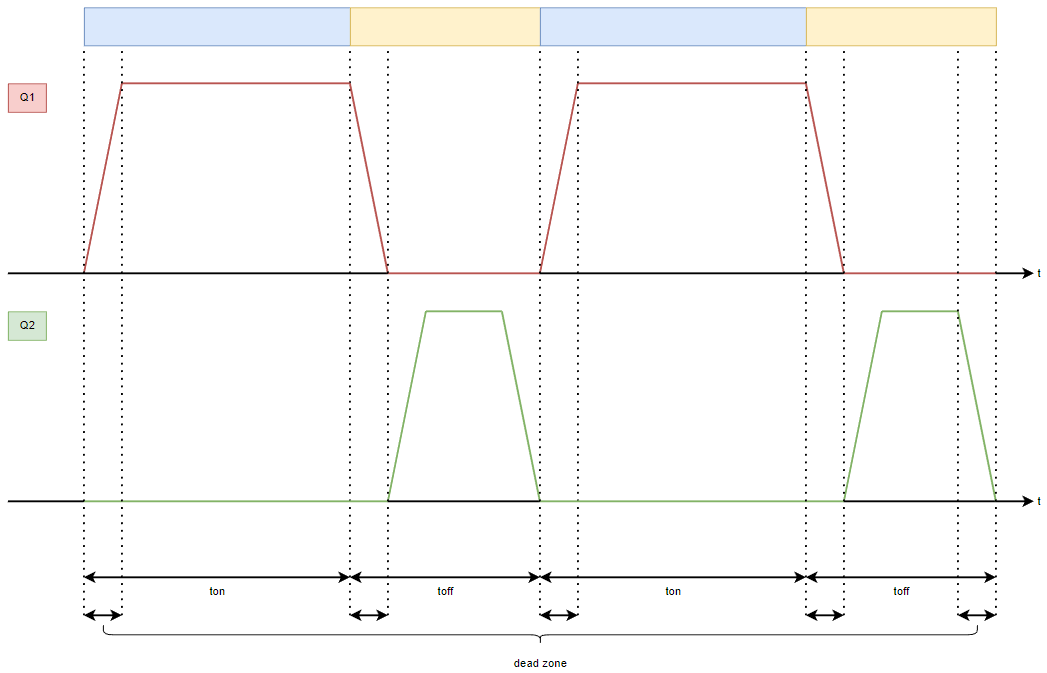
buck-deadzone.png

上图中红色曲线代表Q1的开关状态，绿色曲线代表Q2的开关状态；蓝色区域代表ton而黄色区域代表toff时间阶段。我们注意到曲线具有一段斜坡区域，这是因为开关器件并非严格的是实现了理想的继电器特性，开通和关断的状态转换过程需要一段时间，那么不难想象，假设红色曲线和绿色曲线在同一时刻开始切换（例如Q1关断Q2开通）那么一定有一段区域是二者都处于不完全开通状态。那么在这个区域内就会产生电源的对地短路从而损毁元器件，因此我们将Q2的开通延迟一段时间而Q2的关断提前一段时间，这样就能够保证不会出现击穿期，这段时间也就是所谓的死区(Dead Zone)。

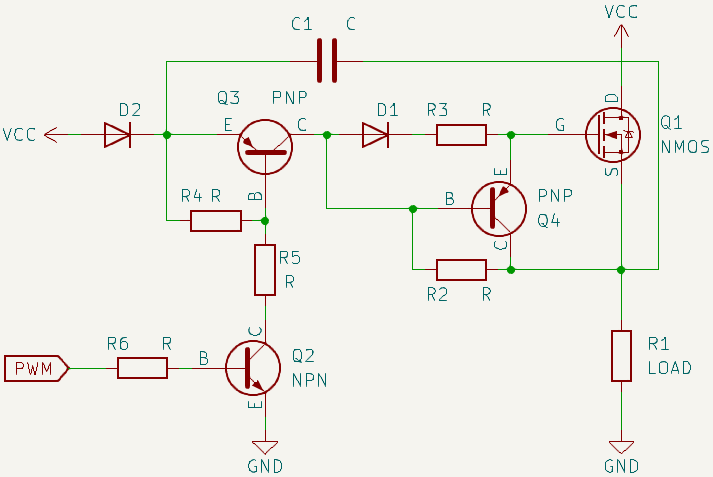
buck-booststrapping.png

观察上图，我们首先要理解为什么需要一个自举升压电路来驱动高侧MOSFET：对于一个处于负载和电源之间的NMOS Q1而言我们会碰到这样一个问题：假设我们给定V_G=V_{CC}那么当NMOS处于关断状态时V_{GS}=V_{CC}-0>V_{GS,th}此时NMOS满足开通条件从而导通，但是导通之后观察通过的电流我们发现：

\begin{aligned}\tag{2-10} i&=\frac{Vcc}{R_{ds,on}+R_1}\\ V_s&=iR_1=\frac{VccR_1}{R_{ds,on}+R_1}\\ V_{GS}&=V_G-V_S=V_{CC}\frac{R_{ds,on}}{R_{ds,on}+R_1}<V_{GS,th} \end{aligned}

这样以来随着MOSFET的导通，反而不满足导通条件，这样就会导致电路无法工作，因此我们要面对的核心问题就是：如何在Q1.S点电平已经被拉升到VCC附近的时候还能在Q1.G点维持一个大于导通电平阈值的高电压（然而并不能高一点点，那样会导致导通电阻很大，我们需要考虑让这个导通电压处于较高的状态）维持Q1的导通状态，并且在需要的时候使其完全关闭，我们先将电路进行一个划分：

  • 电容C1是自举升压(Bootstrapping)电路的核心，即利用电容两侧电压不会突变的原理在Q1开通Q1.Source被拉高后将C1上存储的电荷灌入Q1.Gate维持开通

  • 二极管D2用于防护C1的高电压倒灌到VCC电源之中损坏电源

  • R4，PNP三极管Q3共同构成开关A，一旦Q3导通高电平就将通过Q3.Collection灌入到Q1.Gate开通NMOS

  • R2，PNP三极管Q4共同构成开关B，一旦Q4导通那么Q1.Gate上的高电平就将泄放到Q1.Source上从而无法维持足够的V_{GS}用于开通Q1

  • R5，R6，NPN三极管Q2共同构成开关C，将PWM上的电平转换为开关A和开关B的逻辑状态从而控制NMOS的开通和关断

  • R3用于限制通入Q1.Gate的电流，如果灌电流过大可能损毁Q1.Gate

  • D1用于防止Q1.Gate上的电荷不经过开关B直接通过Q4.Base，R2泄放

当PWM电平为逻辑低时：

  • Q2.Base为低电平，NPN三极管无法导通

  • Q3.Base被R4拉高到Q3.Emit，PNP三极管无法导通

  • 如果此时Q1已经导通，可以看到Q4.Base被R2拉至Q1.Source电平，而Q4.Emit仍旧为Q1.Gate电平，Q4的EB与EC结正向偏置开通Q4，这样Q1.Gate电平通过Q4泄放到Q1.Source上无法维持开通电压，Q1关断

  • 如果Q1此时并未导通将维持关断状态，因此PWM电平为逻辑低时一定关断Q1

  • 由于Q1关断，Q1.Source被LOAD拉低，或者在其他状况中，这个引脚处于“浮地”状态，因此C1能够被VCC通过D2充电至V_{CC}-V_{D2}电压

当PWM电平为逻辑高时：

  • Q2.Base为高电平，NPN三极管导通并且通过R5将Q3.Base拉低

  • Q3.Base被拉低导致PNP三极管Q3导通，C1高电压端也就是Q3.Emit端电平通过Q3的EC结，D1二极管，R3电阻灌入Q1.Gate

  • 此时Q4.Base被拉高到Q3.Collection而Q4.Emit是Q3.Collection经过D1压降的，因此Q4的EB结反向偏置无法开通，Q1.Gate上的电荷无法泄放到Q1.Source上

  • 此时Q1.Gate与Q1.Source的压差是V_{C1}-V_{Q3.EC}-V_{D1}，也就是无论Q1是否开通即Q1.Source电压是否被拉高由于C1两端电压无法突变Q1.Gate都能维持开通Q1所必要的高电平

  • 当然Q1.Gate上的高电平并不是无限维持的，当C1存储的电荷释放完毕之后Q1就将断开，但是一般C1之中存储的电荷足够Q1.Gate在t_{on}期间的耗散

通过以上电路，就能够使PWM电平成功的控制Q1的开通和关断，避免了高侧NMOS驱动中Gate电位不足导致开通失败的问题。以上展示的是使用分立元件构建自举升压电路的原理图，然而各个电阻阻值的选择以及三极管型号的选择都会影响实际的电路性能，在实际应用过程之中我们一般使用集成的半桥驱动电路，例如EG3013https://so.szlcsc.com/global.html?k=C5138297完成半桥控制。

在现代的半桥控制之中，一般来说都会使用“带有死区控制的PWM互补信号”接入半桥驱动芯片，例如STM32单片机的“高级定时器”就有这一功能和打包好的库函数可以直接调用，甚至某些半桥驱动芯片就内置了这种功能，然而使用完全的分立元件和逻辑门也不是不能完成这样的功能，并且其中的死区时间是可以配置的：

buck-complementary.png

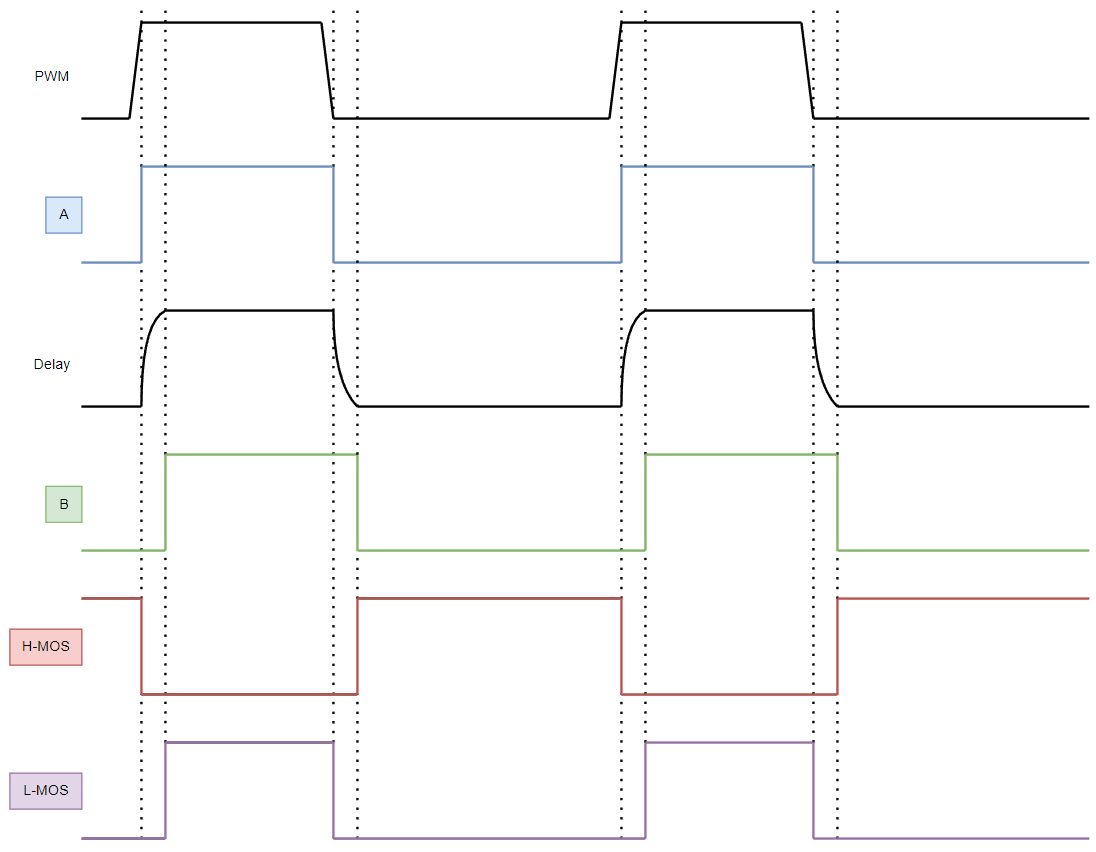
buck-pwm.png

上图之中的电路就将一列PWM信号转换为了带有死区的两路互补PWM信号，也就是H-MOS和L-MOS分别控制半桥的高侧开关管和低侧开关管的状态。Delay代表从施密特触发器U1经过RC延迟电路输入到施密特触发器U2的信号，A和B分别代表施密特触发器U1和U2的输出信号。可以看到通过调整RC的值就能够调整Delay信号充放电的时间常数，就可以决定死区的长短。

3.BUCK变换器扩展内容

前两节之中主要讨论了DC-DC开关电源的基础概念，BUCK转换器的基础结构和相关元件选型的依据和原理，但是最为重要的一些事情例如：面对不甚稳定或者宽压范围的输入电平如何稳定的得到输出电平，BUCK变换器效率低或者出现明显的过冲现象应当怎么解决？本节主要讨论这些问题之中的三个常见问题：

  • BUCK变换器的工作状态也就是常说的CCM-BCM-DCM以及如何判别和控制工作点

  • BUCK变换器的各个环节和元件上的损耗以及如何计算出工作效率

  • 如何构建BUCK变换器的控制系统，在已有的控制系统之中如何处理环路补偿问题

a.系统工作状态控制

首先我们使用Simulink之中的Simscape工具箱搭建一个BUCK电路：

buck-simu-open.png

  • BUCK变换器设计输入电源12V，宽压输入最大值为24V内阻100mΩ，使用一个DC Voltage Source和一个电阻模拟

  • 设计输出电压5V，额定电流3A，负载使用一个电阻代替，调节电阻阻值就能够调节负载电流

  • 暂且使用异步整流，使用二极管续流，正向压降0.7V，正向导通电阻1mΩ

  • N-MOSFET的开关管Gate端接入一个DC-DC PWM Generator模块，根据输入输出电压比例设定占空比为5/12，开关频率500kHz

  • 假设控制电流纹波率20%，计算输出电感感值为13.2uH，取15uH

  • 假设控制输出电压纹波为100mV也就是4.95-5.05V输出，纹波率为2%，计算输出电容容值为1.5uF左右，但是这里考虑到后续要加入闭环控制，为了让闭环控制的控制环路频率以及LC震荡频率不影响性能，这里适度增大到22uF

  • 输入电容这里因为使用了理想电源不做具体要求，直接使用22uF

根据负载电阻的不同，平均输出电流不同，当满负载(3A)时：

buck-CCM.png

可见以最大输入24V计算的电感感值在12V输入条件下表现出色，控制纹波率大概在10%左右，然而当我们升高负载电容容值，从而使输出电流下降时就会出现这样的现象：

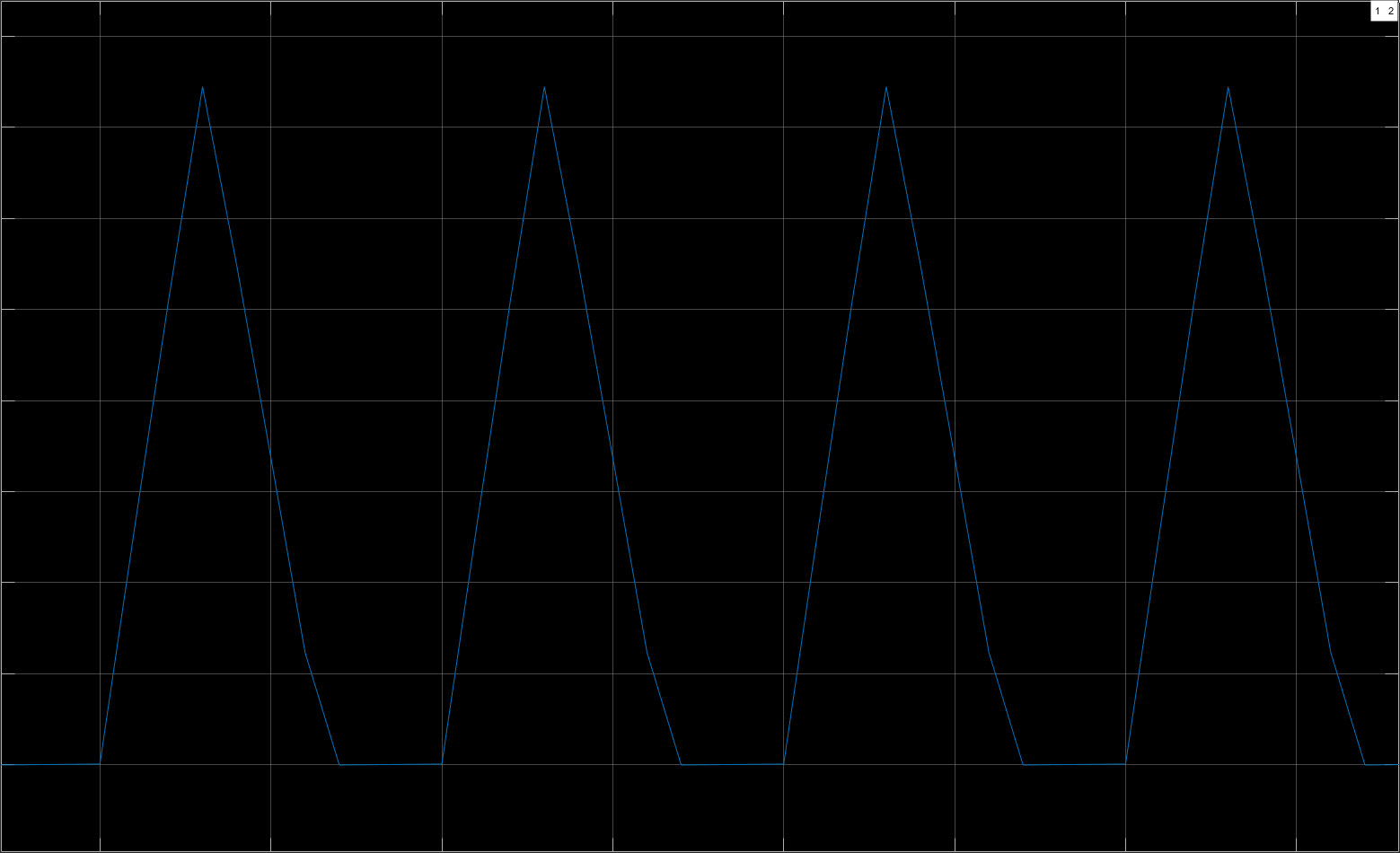
buck-DCM.png

可以看到，在开通相期间电流正常上升，但是在关断相期间，电流提前下降到0值，又因为二极管不允许反向导通导致出现某段时间的电感0电流状态，而我们略微回调电阻值就可以得到这样一种临界状态，也就是在电流值下降到0时恰好转换为开通阶段：

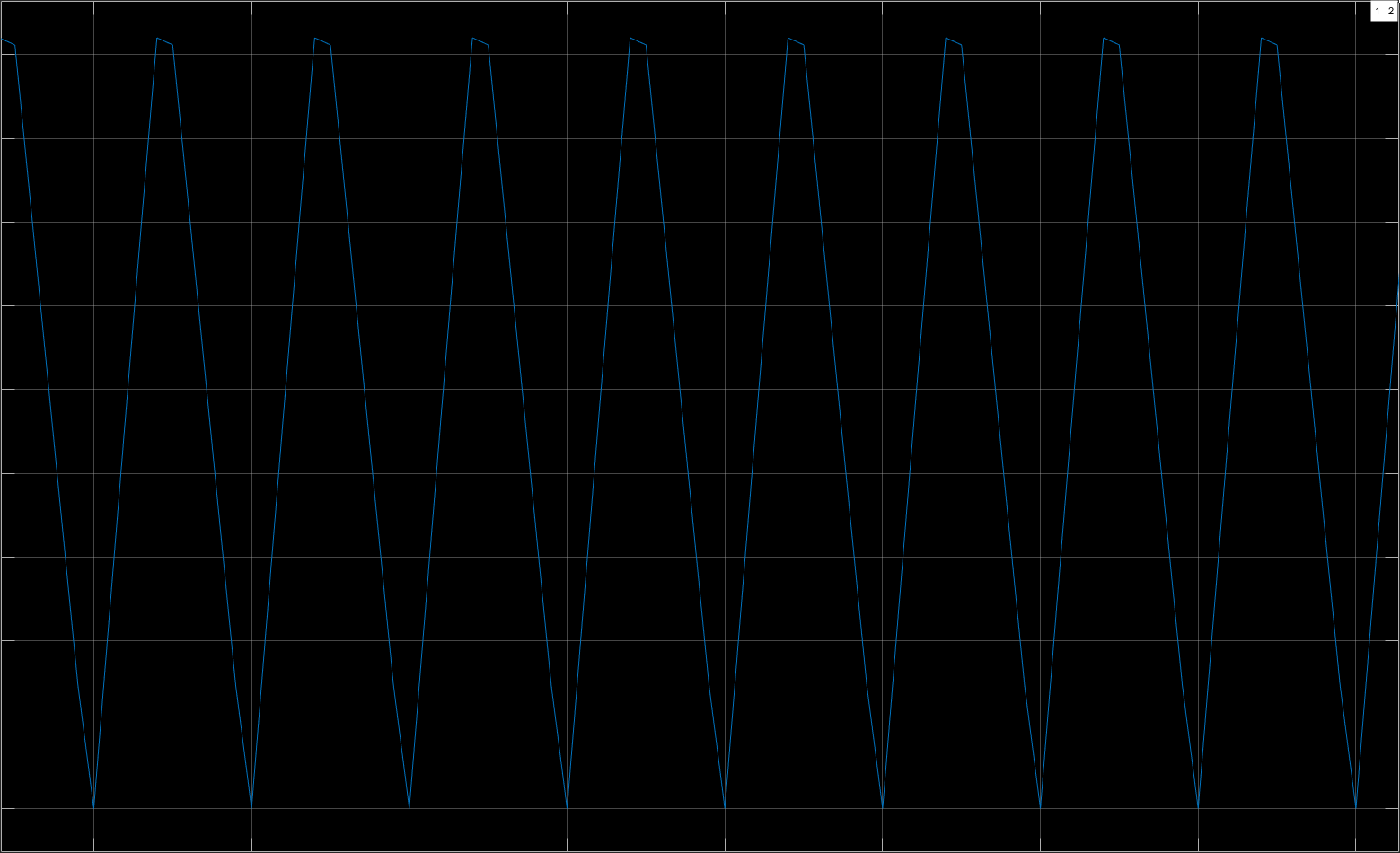
buck-BCM.png

很显然，我们需要警惕第二种持续电感值为0的状况，具体原因下文详述，但是这里我们首先来看临界时的负载电流，我们需要避免变换器工作在此种状态之下。很显然，电流的变化量为前文计算出的I_{ripple}而处于临界状态时显然电流的峰峰值就是这一纹波值，那么可以断定此时的纹波率到达最大的200%，那么临界电流就是：

\tag{3-1} I_{Boundary}=\frac12I_{ripple}=\frac{V_{in}D(1-D)}{2Lf_{sw}}

通过对于输出电流状况，我们将BUCK变换器的三种基础工作模式如此划分：

  • CCM：连续导通模式(Continuous Conduction Mode)，在此模式下，电感电流始终不会为0，保持单向电流流通，纹波率<200%

  • BCM：临界导通模式(Boundary Condcuction Mode)，在此模式下，电感电流在开关管开通时恰好为0，纹波率=200%

  • DCM：断续导通模式(Discontinuous Conduction Mode)，在此模式下，在关断期电感电流会下降为0并且持续一段时间，纹波率>200%

DCM的缺点有很多，而在讨论缺点之前，前文之中很多的推导都要被推翻，例如说这个时候的输出电压一定会比之前讨论的理论开环输出电压不同，产生期望外的偏差。而DCM模式主要的缺点是：

  • 电流纹波较大，完全偏离设计值，有可能损坏后级电路，对于去耦要求更高，可能需要更大的滤波电容来平滑输出

  • 电流在开关周期内频繁上升下降会容易导致更高的开关损耗和导通损耗

  • 电流的变化率跟高，容易产生高频噪声导致更高的EMI从而增加设计和制造的复杂度

  • 使用异步整流时，电流的断续特性会导致二极管的反向恢复损耗大大增大

  • 轻载时输出功率与损耗功率的比值降低，表现为电源效率大大降低

  • 闭环控制难度大，需要实时跟踪电感电流的的变化，增加了设计复杂性

  • 电感电流将为0时在某些极端状态下可能出现电容上积攒的能量通过电感和开关管的续流二极管倒灌到电源出现意料之外的状况

  • 此时LC的寄生参数可能导致LC电路产生高频振荡

我们现在对仿真电路做一些更改，将异步整流变换为同步整流，带有死区的PWM互补信号通过上文的电路产出，Simulink之中的MOSFET不需要考虑高端开通的困难，并且加入对于输出电压的PI控制：

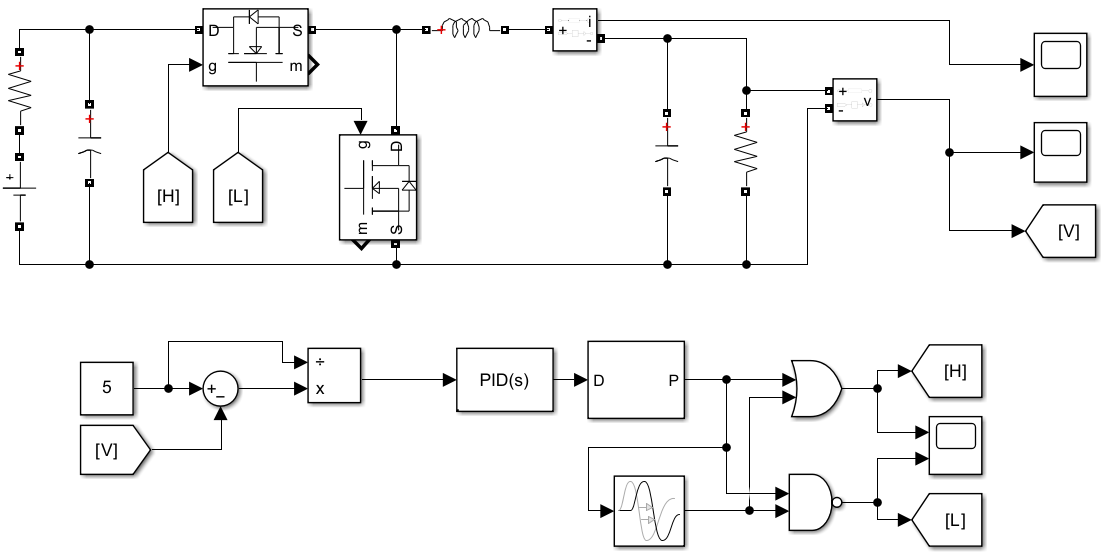
buck-simu-close.png

简单设定PI参数（事实上真正为了可行性分析进行的仿真应当好好调整这部分参数）在额定输出功率5V3A情况下的输出电压以及电感电流如下所示，达到了对于纹波电流和纹波电压的要求，并且在上电3ms后进入稳态，瞬态响应性能及格：

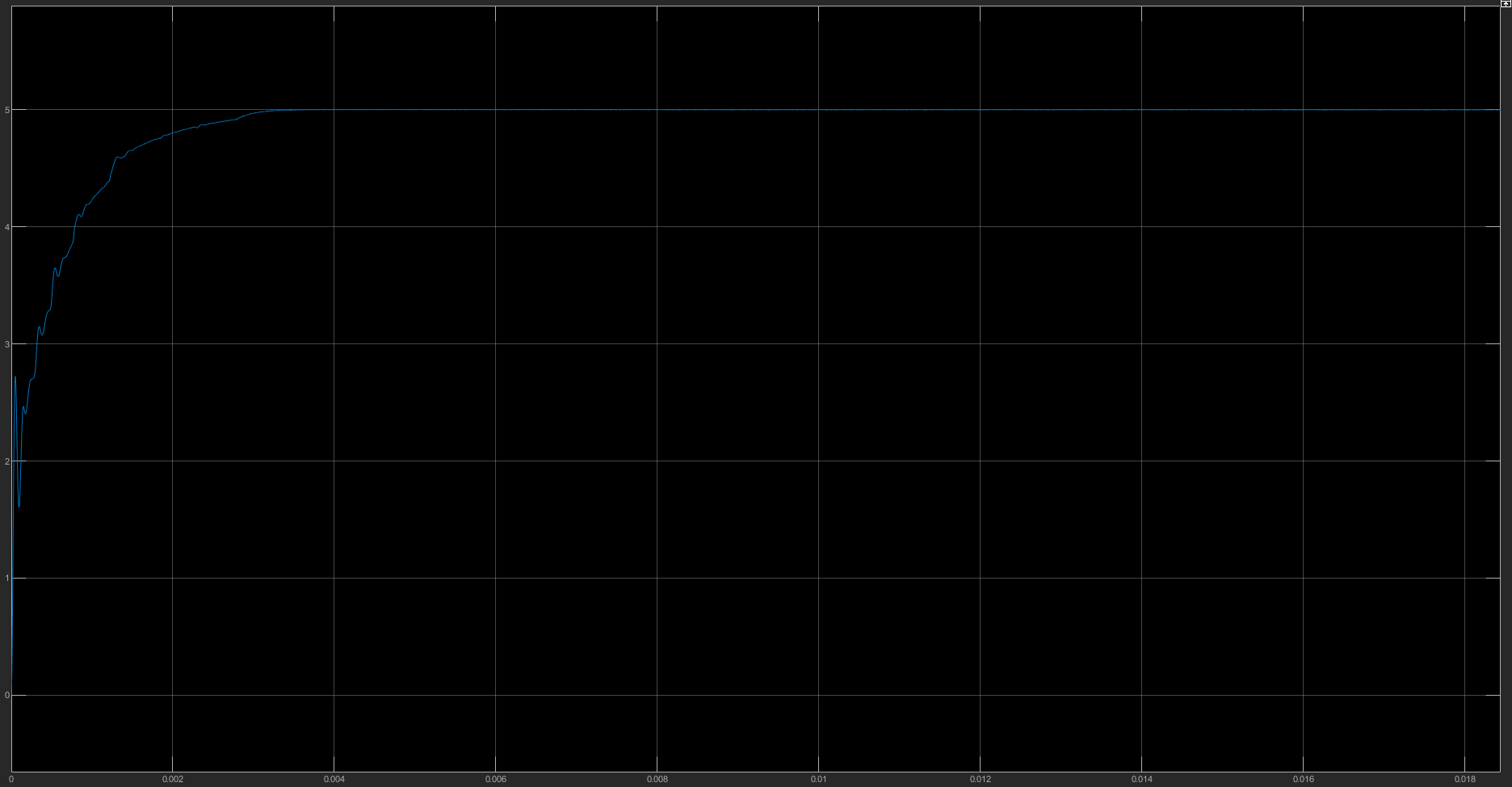
buck-Vccm.png

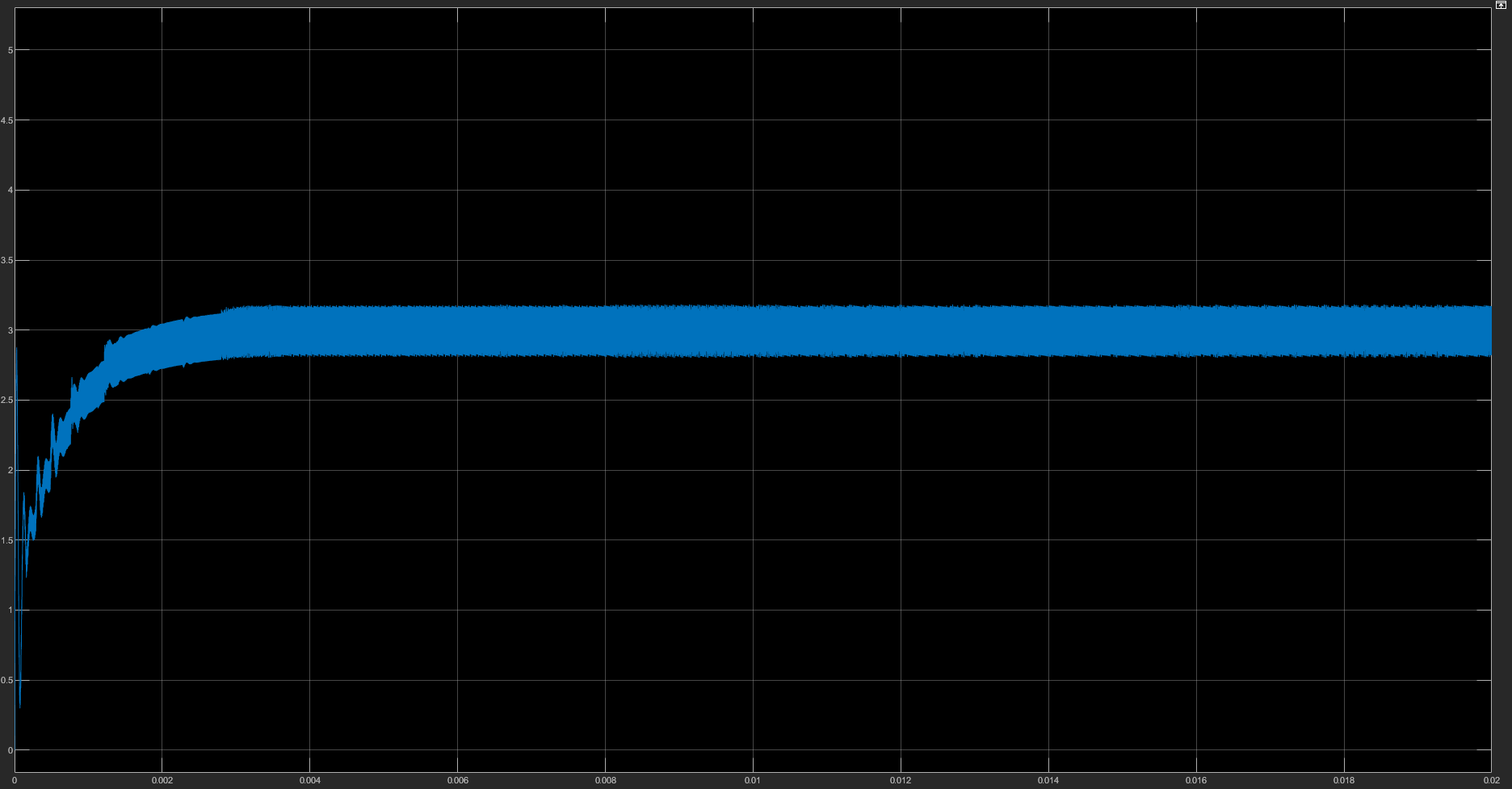
buck-Iccm.png

而由于MOSFET双向导通的特性，在高侧开关（主开关）关断期，即使出现电流触0也可以反向导通电流，让电感上的电流反向流通，这种控制模式叫做FCCM，也就是强制连续导通模式(Forced Continuous Conduction Mode)，下图就展示了上文中的仿真系统在轻载模式下的电感电流图像：

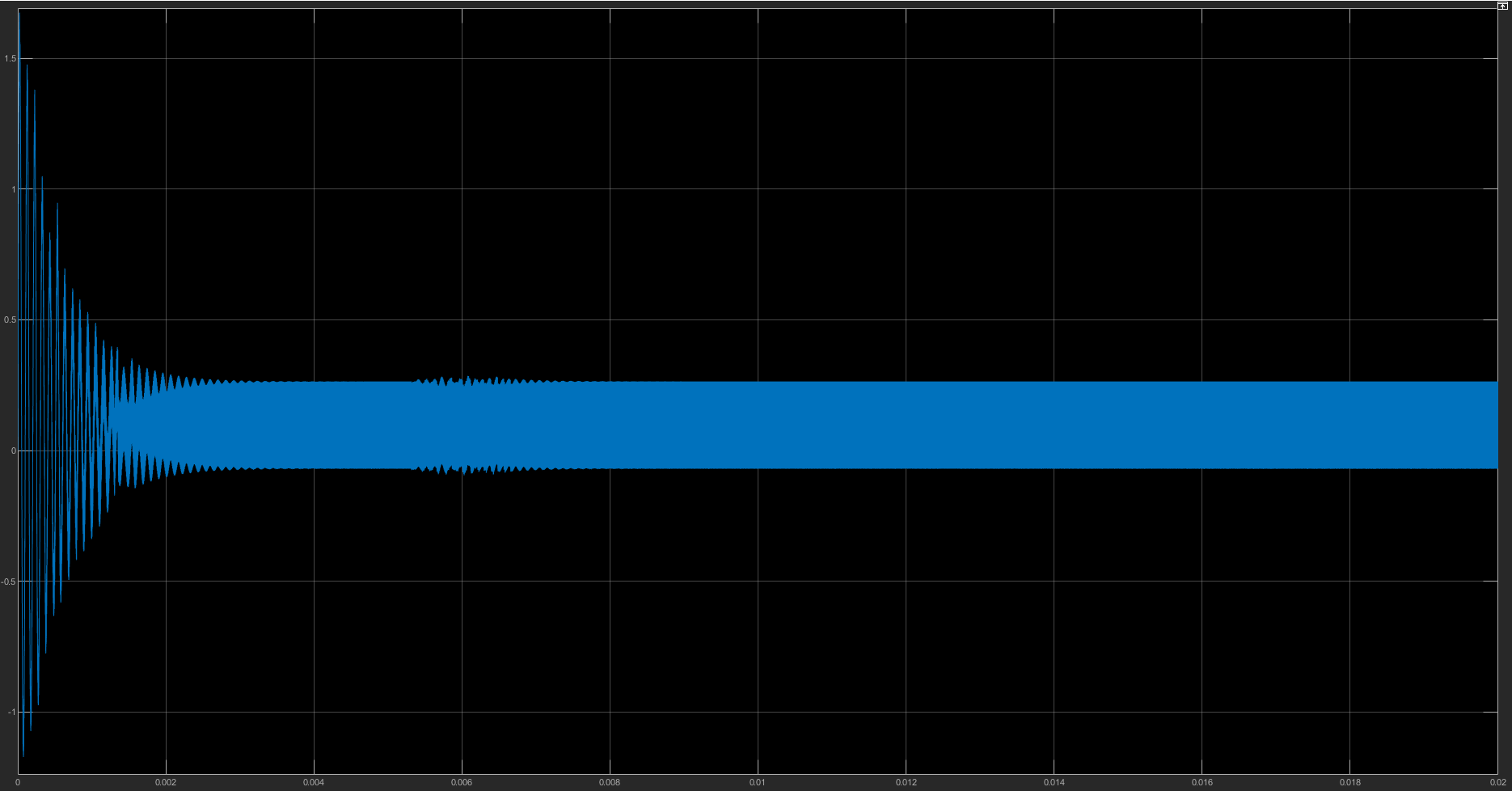
buck-FCM.png

这样做的优点在于：

  • 不必根据轻重负载调整PWM信号以及生成PWM信号的策略，这对于硬件实现和控制策略的开发和实施复杂度大大减轻了压力

  • 在 FCCM 模式下，电感电流不会降到零，输出电压纹波会更小。较低的电流纹波和电压纹波使得 FCCM 模式适合对电压要求较高的应用，尤其是对输出纹波要求严格的系统

  • 在负载突变（如从轻载切换到重载）时，FCCM 模式能更快地响应，因为电感电流始终不为0，可以更快地增加输出功率，从而减少负载瞬态响应时间

  • FCCM 模式下电流连续，有助于抑制 EMI。对于需要较低噪声的应用，例如无线通信设备、精密模拟系统，FCCM 模式可以有效降低 EMI，简化滤波器设计

  • 在 FCCM 模式中，开关频率通常固定，即使负载变化，PWM 控制器也维持恒定的频率输出。这有助于设计输出滤波器，因为滤波器可以针对固定频率优化

除了同步整流+FCCM逆向电流的可能性，还有PSM和PFM两种模式：PSM（Pulse Skip Modulation） 和 PFM（Pulse Frequency Modulation） 是电源管理中常用的两种轻载控制模式，主要用于提高轻载效率。它们在轻载条件下通过调整脉冲模式或频率来减少开关损耗，进而提升电源效率。

  • PSM 脉冲跳跃调制法：

    • 工作原理：

      • 在 PSM 模式下，系统根据负载需求输出一定的脉冲序列

      • 当负载较轻时，如果输出电压已经达到设定值或略高于设定值，控制器会停止开关操作，使输出电压逐渐下降

      • 当输出电压降到设定阈值以下时，控制器会重新开启开关操作，产生脉冲，以便重新将输出电压拉升到设定值

    • 优势1：在轻载下大幅减少开关频率，降低开关损耗，提升效率

    • 优势2：在负载变化不频繁或输出电压纹波要求不严格的场合表现良好

    • 劣势1：会产生较大的输出电压纹波，因为控制器是通过间歇性脉冲来保持电压

    • 劣势2：由于跳脉冲产生的间歇性工作，频谱特性较复杂，可能会增加系统的 EMI

  • PFM 脉冲频率调制法：

    • 工作原理：

      • PFM 模式的核心在于调节频率。当负载变轻时，控制器会降低开关频率，而不是调整占空比

      • 在轻载下，PFM 通过降低开关频率来降低开关损耗，并保持电感电流在较低水平

      • 当负载变重时，PFM 模式会逐渐提高频率，以应对更大的负载需求

    • 优势1：在轻载下，PFM 通过降低开关频率来降低开关损耗，并保持电感电流在较低水平。

    • 优势2：当负载变重时，PFM 模式会逐渐提高频率，以应对更大的负载需求，控制过程相比于PSM而言比较平滑

    • 劣势：频率调制会使系统的 EMI 特性复杂化，需要设计时额外关注 EMI 控制。

上文所用到的仿真模型为Matlab R2022b-Simulink(需要安装Simscape工具箱)，点击下载SLX文件。

b.变换器损耗(效率)分析

要分析电源的效率，实际上就是分析电源的各个部分各个元器件的工作状态下的损耗问题，这其中我们需要考虑到的部分主要有：

  • 输入电容

  • 开关元器件(例如MOSFET)

  • 续流元件(包括异步整流的被动二极管或者同步整流的开关管)

  • 输出电感

  • 输出电容

  • 反馈控制中的运算电路与采样电路

其中高侧MOSFET的导通损耗为：

\tag{3-2} P_{Q1,on}=I^2_{out}\times R_{ds,on}\times D

同步整流下低侧MOSFET导通损耗如下，其中t_{dead}为PWM死区时间总和：

\tag{3-3} P_{Q2,on}=I^2_{out}\times R_{ds,on}\times(1-D-t_{dead}f_{sw})

不考虑DCM或者说CCM+FCCM模式下的电感导通损耗：

\tag{3-4} P_{L,on}=I^2_{out}\times R_{L,dc}

如果具有电流环(本文使用的仿真系统只有一级电压PID，事实上很可能有U-I串级PID)：

\tag{3-5} P_{sense}=I^2_{out}\times R_{sense}

死区时间Q2体二极管的导通损耗为：

\tag{3-6} P_{Q2,off}=V_{Q2,diode}\times I_{out}\times t_{dead}f_{sw}

由于异步整流本身电源效率不高并且正在退出市场，所以对于异步整流架构中续流二极管的导通损耗和总电荷耗散暂不讨论。

而我们需要注意的是虽然MOSFET是压控元件，但是为了使其达到导通条件需要向其Gate引脚输送一定的电荷达到开通阈值，而为了避免损坏MOSFET通常Gate上还有一个限流电阻，故而MOSFET的导通需要一定时间，此时Drain-Source之间的电压和Drain流过的电流重合产生开通损耗，相应的关断期间也有关断损耗。而由于死区时间的存在，当Q2切换状态时其Drain-Source电压已经相当之低到没有计算必要，因此Q1，Q2同时具有开通需要的驱动损耗，一同计算：

\tag{3-7} P_{driver}=2Q_{gate}\times V_{Driver}\times f_{sw}

而Q1还具有切换状态的损耗：

\tag{3-8} P_{switch}=\frac12V_{in}\times I_{out}\times(t_{open}+t_{close})\times f_{sw}

在此之外还有驱动整个闭环逻辑电路工作的损耗，逻辑电路需要的电平通常通过LDO实现那么也需要计算，以及驱动高侧开关管的自举升压电路的损耗，这些损耗记作P_{Logic}，累计以上所有损耗功率即可算出整体损耗功率进而得出电源效率\eta。

c.环路稳定性与补偿

在很多BUCK变换器的数据手册之中看起来都会在某些引脚上加入几个毫无逻辑可言的电阻和电容，问就是“环路补偿”，“有助于提高性能”那么这是什么意思呢？？？以及在前文的推导过程之中，我们似乎仅仅只在电路原理上分析了BUCK变换器以及参数的选取，但是我们从未从BUCK变换器的性能例如瞬态响应性能或者抗扰性能方面分析，那么在本节之中重点将从器件和电路分析转移到控制系统中来。谈论到一个自动控制系统，我们首先需要对于系统进行建模，也就是我们的受控对象是什么东西：

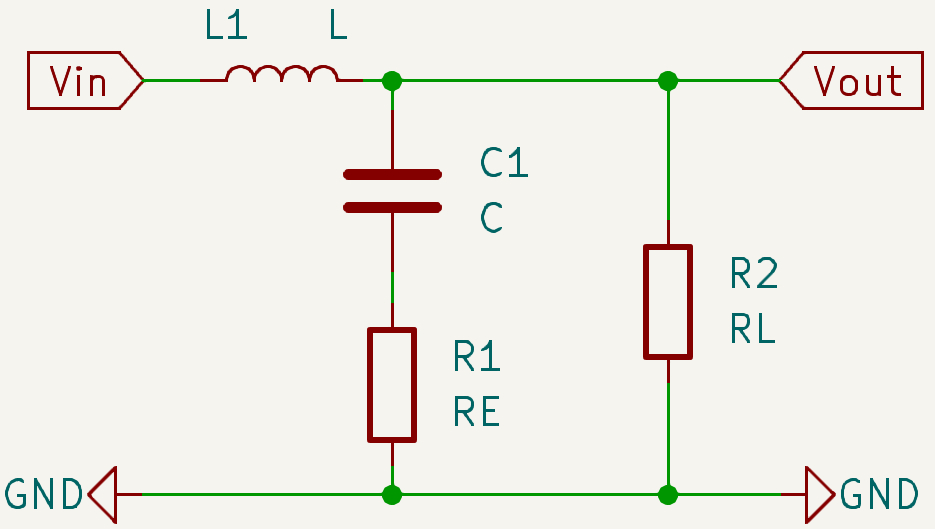
buck-systeml.png

抛去所有乱七八糟的开关器件和续流管（关你是什么东西，去掉这些非线性的器件来分析本质，对于这类系统不需要分析其中的强非线性部分直接进行粗暴的线性化，抓大放小!）我们发现这就是一个带有一个额外电阻器的LC振荡器，之所以这样做有几点考虑：

  • 实质上电感L和电容C都具有ESR等效串联电阻，这两个电阻完全可以归并处理，从物理上是合理的

  • 如果直接忽略掉这个ESR整个系统将会称为一个完全的LC振荡器，传递函数将会是灾难性的1/(s^2LC+1)，我只看到了无限大的谐振峰值，这种非BIBO的系统完全无法接受，别分析了直接参数炼丹吧

  • 为什么使用固定的负载电阻RLOAD代替呢？以复功率和复阻抗的角度来看，负载是容性还是感性还是纯阻性无所谓，因此改变而改变的负载电流(偏离额定电流的)直接作为系统扰动和噪声处理

那么求个传递函数吧：

\tag{3-9} \begin{aligned} G_{Buck}(s)&=\frac{V_{out}(s)}{V_{in}(s)}\\ &=\frac{sCR_E+1}{(1+\frac{R_E}{R_L})LCs^2+(\frac L{R_L}+CR_E)s+1} \end{aligned}

可以看到和我们的预期相符，由于含有一个L和一个C，系统表现出一个二阶阻尼环节和一个一阶微分环节叠加的特征，如果我们认为RE过小可以不加计算的话，那么我们可以获得一个更加简单的系统模型：

\tag{3-10} G_{Buck}=\frac1{LCs^2+\frac L{R_L}s+1}

那么这就是系统开环传递函数的全部了么？让我们回到系统整体的视图上，带入负反馈形成的环路和生成PWM波形驱动BUCK变换器电路的层面来思考这个问题：

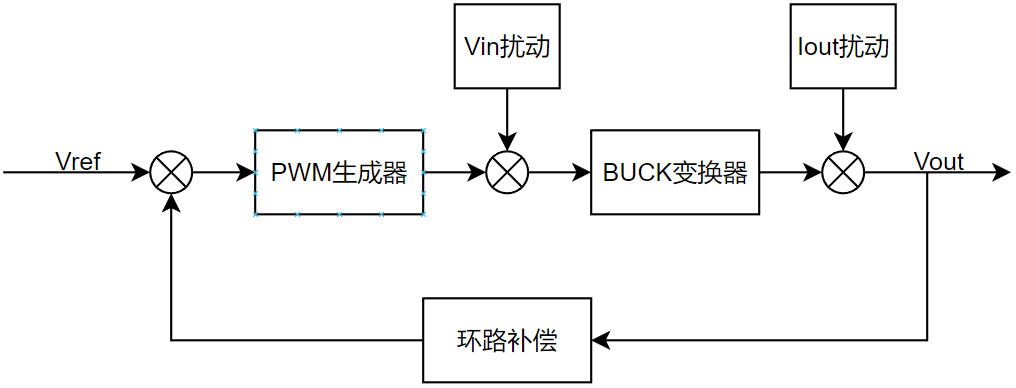
buck-flowchart.png

  • 目标输出电压V_{ref}是系统的输入，在系统分析中我们可以认为这是一个常量，当它改变时认为是一次瞬态阶跃

  • BUCK的实际输出电压V_{out}是系统的输出，也是我们闭环反馈的信号来源

  • 系统主要前向环节有两个，一个是我们已经进行建模的BUCK变换器部分，传递函数记作G_{Buck}(s)

  • 而在BUCK变换器之前是PWM生成器，这个环节在我们考虑系统是“线性连续时不变系统(CLTI)”时这个位置其实是一个非常单纯的比例环节，因为输入到这个环节的占空比在逻辑上会被转换为输入到后续电路的平均电压，那么如果这个环节的输入是占空比D，那么给到后级的电压是V_{in}D，所以这个环节的传递函数是：G_{PWM}(s)=V_{in}

  • 而我们要做的环路补偿环节记作H(s)，我们暂且认为这个环节就是1，因为最简单的闭环就是将实际值直接与设计值做差。而本节的核心任务就是考虑如何将这个环节设计并且通过电路实现

  • 系统的扰动只要有两个：输入电压变化和输出功率（也就是输出电流和常数R_L的变化）

从以上分析之中我们能够得出许多看似无用但是重要的结论：

  • 实际制造问题的物理输入输出，做电学分析的电气输入输出，做控制策略的系统输入输出仅仅具有逻辑推理关系而不具有强硬的对应

  • 对于BUCK变换器的建模本身并不是要将电学的BUCK变换器模拟到数学结构之中来，而仅仅将其设计目的：使输出电压符合占空比控制的输出值而不受到电压输入和负载输出的扰动作为核心——那么目标非常明确，将低频的，不变的，有参考性的信号忠实的输出，给予一个相当大的增益以便闭环调节；将高频的，易变的，带来误差的扰动抑制

  • 环路补偿本身是一个自动控制问题或者说数学问题，使用什么器件或者干脆是MCU软件程序仅仅是实现手段

  • 可以得到系统整体的开环传递函数和闭环传递函数：

\tag{3-11} \begin{aligned} G_{open}&=G_{PWM}G_{Buck}H(s)\\ &=V_{in}\frac{sCR_E+1}{(1+\frac{R_E}{R_L})LCs^2+(\frac L{R_L}+CR_E)s+1}H(s)\\ G_{close}&=\frac{G_{PWM}G_{Buck}}{1+G_{PWM}G_{Buck}H(s)} \end{aligned}

在MATLAB之中绘制H(s)=1时的开环传递函数对数频率特征图(Bode)：

% Define BUCK converter paramter
Vin=12;     % Standard input voltage
Vref=5;     % Desired output voltage
R_E=0.5;    % Capacitor equal serial resistance
R_L=Vref/3; % Desired output current as 3A
C=22e-6;    % Output capacitor
L=15e-6;    % Output Conductor

% Define transfer function
Num=[C*R_E*R_L,1]; % Numerator coefficients
Den=[(R_E+R_L)*L*C,C*R_E*R_L+L,R_L]; % Denominator coefficients
G=Vin*tf(Num,Den);

bodeplot(G)
grid on;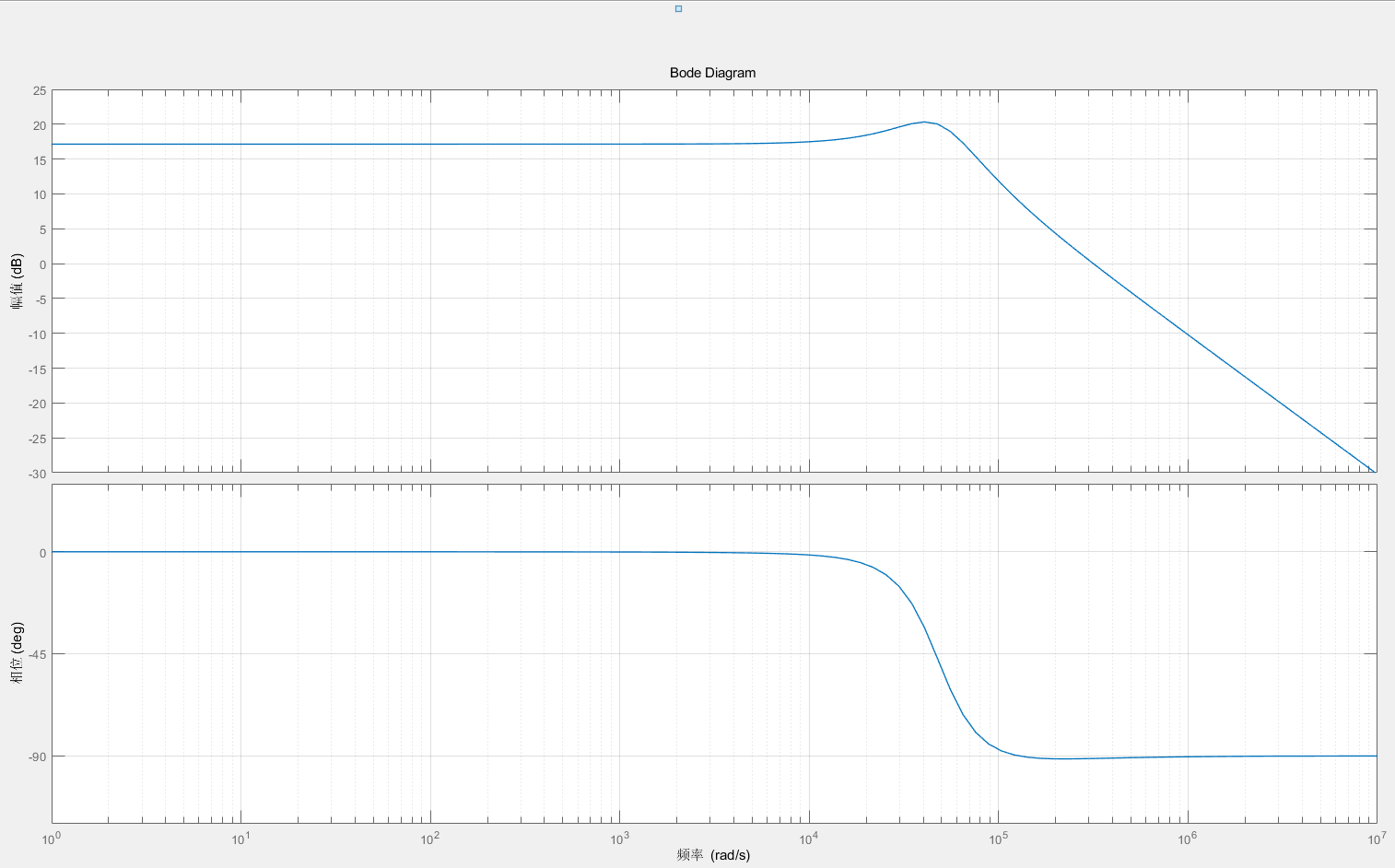

buck-bode.png

可以看到：

  • 系统整体特性符合预期，表现出一个二阶欠阻尼系统特征，在自然震荡频率30k rad/s=4.7k Hz处出现谐振峰

  • 系统相频特性在100k以上表现出略微的相位超前(滞后程度减小，曲线略微上扬）这就是分子上R_E项引起的零点(一阶微分)的特征

  • 系统相位裕度和幅值裕度足够，即使不加入任何补偿系统也是稳定的

  • 问题1：在低频区的增益只有不到20dB，低频区增益太小，环路稳定速度太慢

  • 问题2：穿越频率已经到达200k rad/s左右，太高距离系统PWM开关频率太近，无法很好的抑制高频噪声，极限情况下会共振

在进行真正的环路补偿讨论之前首先明确几个基本概念：

  • 幅频特性曲线的纵坐标单位是dB，B=\log_{10}\frac{S_1}{S_0},S1是实际值，S0是标准值，1dB=10B，所以如果S1=2S0也就是信号强度翻倍，那么计算出来的分贝值就是3dB——所谓的强度翻番分贝+3，这也是为什么很多情境下注重-3dB，也就是这时候信号强度已经相比原信号下降了50%了。同样穿越频率就是0dB对应值，0dB就代表了增益为1，超过穿越频率的部分都是增益抑制区域。

  • 系统的零点给系统的幅频特性在转折频率后带来+20dB的斜率上升，在相频特性上带来90°的相位超前

    • 零点会让大于转折频率的高频信号增益放大，而且频率越高增益越大，这给系统带来性能下降和不稳定隐患，需要剔除

    • 零点由于提升了转折频率后整体Bode的增益值，因此会让dB=0的穿越频率滞后出现，需要剔除

    • 零点令转折频率后的整个相频曲线超前90°，因此带来更大的相位裕度，转折频率越早相位裕度提升越大，需要保留

  • 系统的极点给系统的幅频特性在转折频率后带来-20dB的斜率下降，在相频特性上带来90°的相位滞后

    • 极点会让大于转折频率的高频信号增益缩小，可以利用零极点对消从系统中剔除不需要的表现出恶劣特征的零点

    • 极点由于减小了转折频率后整体Bode的增益值，可以很好的抑制高频噪声并且让穿越频率提前，远离系统PWM工作点

    • 极点由于在转折频率后将相频曲线滞后90°因此会减小相频裕度，要避免在穿越频率附近出现导致系统失去稳定性

那么我们开始设计一个系统的环路补偿，首先就是要确定穿越频率，这个值一般是[0.05,0.2]f_{sw}为可接受的值，考虑开关频率100kHz，我们这里取折中值0.1倍的PWM开关频率，也就是：

f_c=\frac1{10}f_{sw}=10kHz=20k\pi\ rad/s\approx62.8k rad/s\tag{3-12}

下一步是提高系统的相位裕度，并且出于零极点对消抑制谐振峰的考虑，应当将这两个零点布置在系统额自然震荡频率附近，那么一个零点转折频率配置在谐振频率下，另一个零点出于提高相位裕度的考虑配置在小于谐振频率这里配置在0.1倍下：

\tag{3-13} \begin{cases} f_{z1}=\omega_n=30k\ rad/s\\ f_{z2}=\frac1{2}\omega_n=15k\ rad/s \end{cases}

两个极点要避开穿越频率的同时需要完成这样两件事：1.抑制ESR带来的零点，这是我们不希望看到的，因此配置在ESR-C的RC振荡频率处;2.抑制超过穿越频率的高频噪声，因此配置为2倍穿越频率：

\tag{3-14} \begin{cases} f_{p1}=\frac{1}{2\pi\cdot R_E\cdot C}\\ f_{p2}=2f_c \end{cases}

然而此时的穿越频率不一定是我们想要的f_c，这时候将Bode幅频曲线整体进行上下移动，也就是给定一个初始积分器极点配合一个增益即可达到我们想要的效果：

\tag{3-15} G_p(j\omega)=\frac K{j\omega}\Rightarrow L_p(\omega)=20\lg K-20\lg\omega

之前MATLAB绘图之中用到的BUCK变换器传递函数为：

\tag{3-16} \begin{aligned} G_o(s)&=G_{PWM}G_{Buck} \\&=V_{in}\frac{sCR_E+1}{(1+\frac{R_E}{R_L})LCs^2+(\frac L{R_L}+CR_E)s+1}\\ &=\frac{2.2\times10^{-4}s+12}{7.15\times 10^{-10}s^2+3.33\times10^{-5}s+1.67}\\ H(s)&=G_p(s)G_{p1}(s)G_{p2}(s)G_{z1}(s)G_{z2}(s)\\ &=\frac{K}{s}\frac{1}{2\pi R_ECs+1}\cdot\frac{1}{\frac1{2f_c}s+1}\cdot(\frac1{\omega_n}s+1)(\frac1{\frac{\omega_n}{2}}s+1)\\ L(\omega)&=20\lg K-20\lg\omega\\&\quad-20\lg\sqrt{(2\pi R_EC\omega)^2+1}-20\lg\sqrt{(\frac{\omega}{2f_c})^2+1}\\&\quad+20\lg\sqrt{(\frac{\omega}{\omega_n})^2+1}+20\lg\sqrt{(\frac{2\omega}{\omega_n})^2+1}\\ L_o(f_c)L(f_c)&=0 \end{aligned}

于是使用如下脚本直接计算出K并且绘制校正补偿后的Bode图：

% Define BUCK converter paramter
Vin=12;     % Standard input voltage
Vref=5;     % Desired output voltage
R_E=0.5;    % Capacitor equal serial resistance
R_L=Vref/3; % Desired output current as 3A
C=22e-6;    % Output capacitor
L=15e-6;    % Output Conductor

% Define transfer function
Num=[C*R_E*R_L,1]; % Numerator coefficients
Den=[(R_E+R_L)*L*C,C*R_E*R_L+L,R_L]; % Denominator coefficients
G=Vin*tf(Num,Den);

% bodeplot(G)
% grid on;

% Define H(s) constants
w_n=3e4;        % natural frequency
f_c=6.28e4;     % target cut-off frequency
G_p1=tf(1,[6.28*R_E*C,1]);
G_p2=tf(1,[0.5/f_c,1]);
G_z1=tf([1/w_n,1],1);
G_z2=tf([2/w_n,1],1);
g=G*G_p1*G_p2*G_z1*G_z2*tf(1,[1,0]);

% Solve K needed by target f_c
F_c=1i*f_c;
g_fc=evalfr(g,F_c);
K=1/abs(g_fc);

% Draw Bode
GH=K*g;
bode(GH)
grid on;

% Calculate phase margin
[GM,PM,Wcg,Wcp]=margin(GH);
disp(['Phase Margin(deg)= ', num2str(PM)]);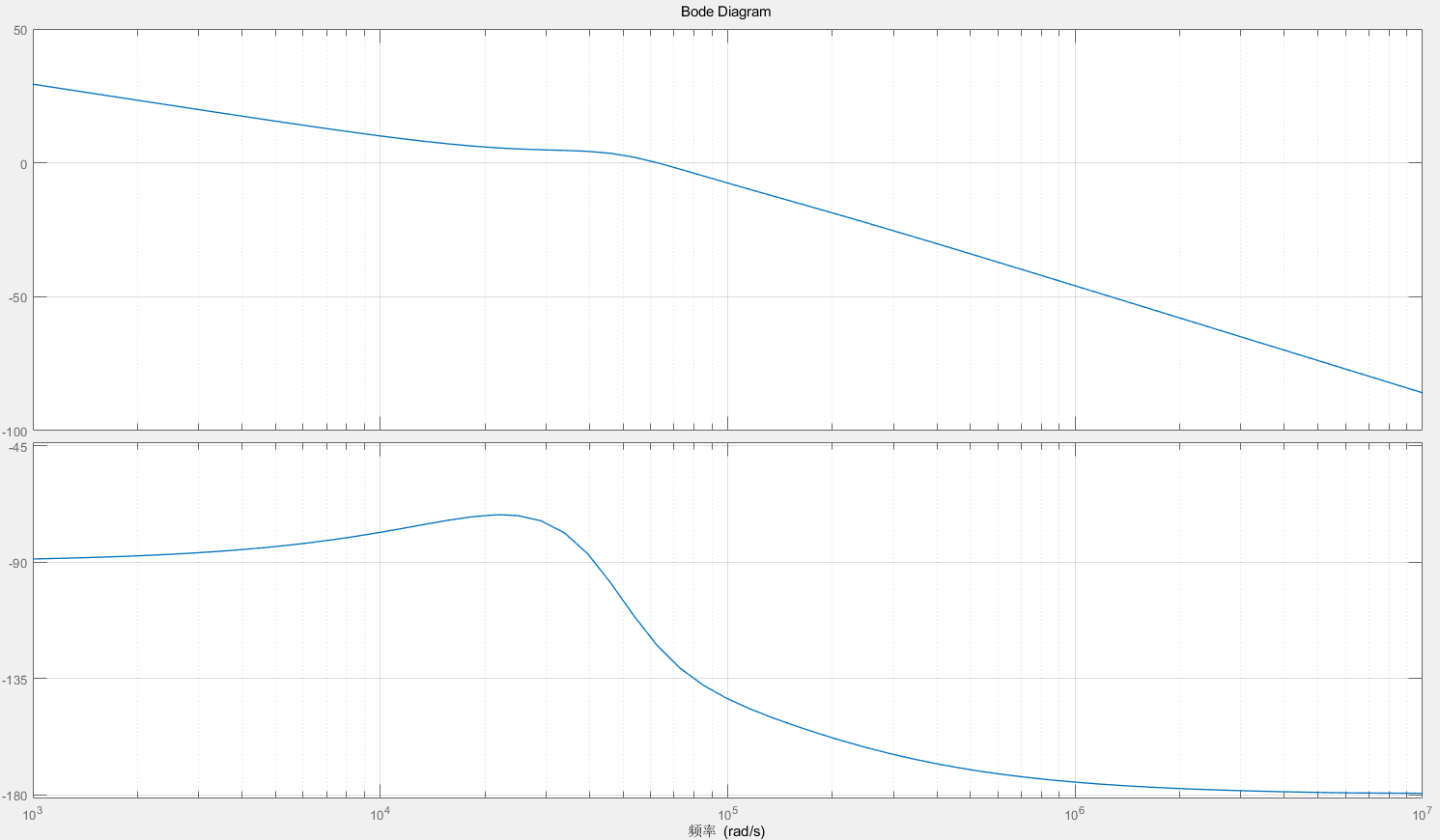

buck-bode-correction.png

可以看到校正后：

  • 截止频率落在62.8k rad/s 也就是 10kHz，原理PWM工作频率，免除了共振的可能性

  • 零点1有效的削除的系统LC部分的自然震荡谐振峰

  • 度过截止频率后系统的放大增益快速下降，拥有良好的高频抑制特性

  • 系统的低频放大增益大大上升，能够拥有更加良好的瞬态响应性能

  • 相位裕度57.6°左右，大大大于工程经验上的安全值45°，带来良好的抗扰性能

  • 相位延迟与-180°擦肩而过，系统幅值裕度无穷大，在任何频率的BIBO信号下都不会出现增益不稳定

通过以上推理和验证，我们现在确信进行环路补偿的办法在数学或者说控制理论上是有效且可替代一般的PID控制器的，那么这个结构如何从具体的电路上实现呢？总不能什么都靠MCU软件运算然后依赖高频环路模拟连续系统吧？那么我们来看以下三个运算放大电路就是三种常见的环路补偿电路的实现：

buck-circuit.png

对于左侧的运算放大电路我们称之为I型环路补偿，它仅仅提供一个带增益的积分器：

\tag{3-17} \begin{cases} \frac{V_{out}-V_-}{R_1}+C_1\frac{d(V_--V_{comp})}{dt}=0\\ V_+=V_-=V_{ref} \end{cases}\Rightarrow \frac{V_{comp}(s)}{V_{out}(s)}=\frac1{sR_1C_1}\Rightarrow K=\frac1{R_1C_1}

对于中部的运算放大电路我们称之为II型环路补偿，它提供一个增益积分器的同时还额外提供一对零极点：

\tag{3-18} \begin{aligned} \begin{cases} \frac{V_{out}-V_-}{R_1}+\frac{V_--V_{ref}}{Z_1}=0\\ V_+=V_-=V_{ref}\\ Z_1(s)=\frac1{sC_1}\parallel(R_2+\frac1{sC2}) \end{cases} &\Rightarrow \frac{V_{comp}(s)}{V_{out}(s)}= \frac{R_2C_2s+1}{sR_1[R_2C_1C_2s+(C_1+C_2)]} \\&\Rightarrow \begin{cases} \omega_{z_1}=\frac1{R_2C_2}\\ \omega_{p_1}=\frac{C_1+C_2}{R_2C_1C_2}\\ K=\frac1{R_1(C_1+C_2)} \end{cases} \end{aligned}

对于右侧的运算放大电路也就是上文使用的，称为III型环路补偿，提供两对零极点和一个增益积分器：

\tag{3-19} \begin{aligned} \begin{cases} \frac{V_{out}-V_-}{Z_2}+\frac{V_--V_{ref}}{Z_1}\\ V_+=V_-=V_{ref}\\ Z_1(s)=\frac1{sC_1}\parallel(R_2+\frac1{sC_2})\\ Z_2(s)=R_1\parallel(R_3+\frac1{sC_3}) \end{cases} &\Rightarrow \frac{V_{comp}(s)}{V_{out}(s)}= \frac{(R_2C_2s+1)[C_3(R_1+R_3)s+1]}{s(R_1R_3C_3s+R_1)[C_1C_2R_2s+(C_1+C_2)]}\\ &\Rightarrow\begin{cases} \omega_{z1}=\frac1{R_2C_2},&\omega_{z2}=\frac1{C_3(R_1+R_3)}\\ \omega_{p1}=\frac1{R_3C_3},&\omega_{p2}=\frac{C_1+C_2}{C_1C_2R_2}\\ K=\frac1{R_1(C_1+C_2)} \end{cases} \end{aligned}

这些环路补偿运放电路输出的是一个电压值，与频率为f_{sw}幅值为[0,V_{in}]的锯齿波做比较输入电压比较器，最终输出PWM波驱动BUCK主电路使后级具有功率输出，这样就完成了环路补偿模式下的闭环BUCK电路控制，能够具有较好的瞬态响应特征和抗干扰性，干扰可能来自输入电压的抖动和负载变动引起的输出电流波动。

[Design Pattern 0...
OLED-SSD1306手册分析与...

评论